6

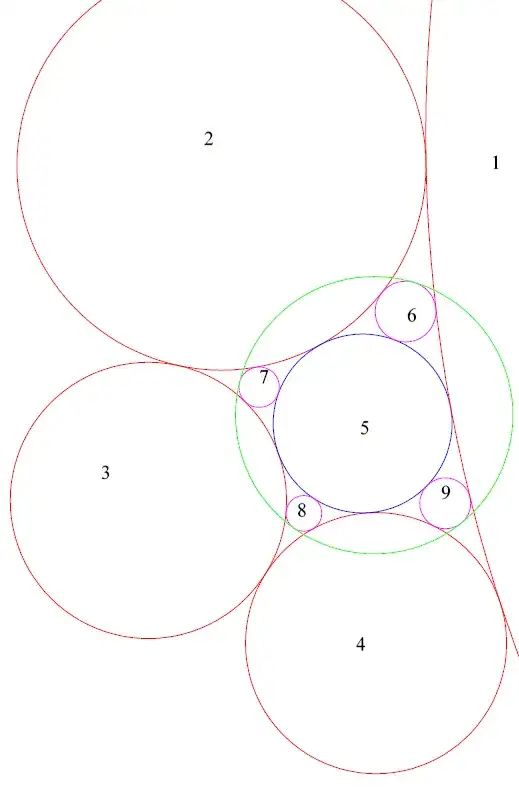
Problem $1:$ Let four (red) cirles $1, 2, 3, 4$ such that $1$ touching $2, 2$ touching $3, 3$ touching $4, 4$ touching $1$ and $1, 2, 3, 4$ touching (blue) circle $5.$ Construct four purple circles $6, 7, 8, 9$ such that: $6$ touching $1, 2, 5; 7 $touching $2, 3, 5; 8$ touching $3, 4, 5; 9$ touch $4, 1, 5. $Then exist a circle touching with four circles $6, 7, 8, 9$ (green).

enter image description here

Problem $2:$ Let three green circles $1, 2, 3$ and a circle purple $4.$ Construct two circles of Apollonius touching $1, 2$ and $4.$ These two circles of Apollonius touching $4$ at two points $A, B$. Construct two circles of Apollonius touching $2, 3 ,$ and $4,$ These two circles of Apollonius touching $4$ at two points $C, D$ Construct two circles of Apollonius touching $3, 1 ,$ and $4,$ These two circles of Apollonius touching $4$ at two points $E, F.$ Show than $AB, CD, EF$ are concurent.

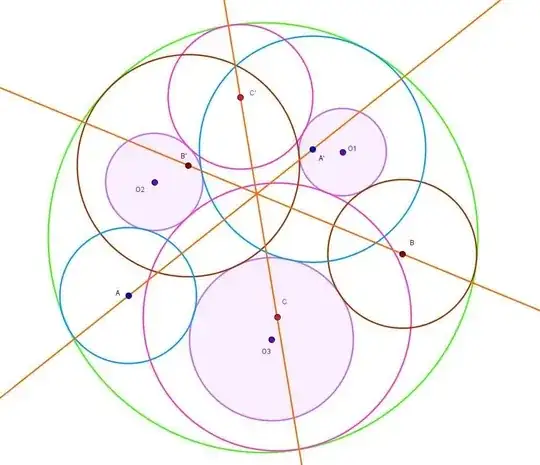
enter image description here

Problem $3:$ (by Telv Cohl) Show that $AA', BB', CC'$ are concurrent:

enter image description here

Oai Thanh Đào
  • 1,366
  • 5
    I don't see the relation between the $1^{st}$ and $2^{nd}/3^{rd}$ question. In general, unrelated questions should be asked separately and some motivation/context should be provided. In any event, problem 1 can be solved easily by a circle inversion with respect to the touching point between circle $5$ and one of the circles $1,2,3,4$. – achille hui Dec 17 '15 at 06:39
  • Thank to dear @achillehui , 2nd and 3rd are in one configuration. 1st is different. But they are some problems of ten circles – Oai Thanh Đào Dec 17 '15 at 06:46

2 Answers2

4

Inversion to Answer the First Question

If we invert the first image at the point of tangency of circles $1$ and $5$, we get

enter image description here

Due to the symmetry of the situation of circles $1$-$9$, it is easy to see that a green circle can be found that is tangent to circles $6$-$9$.

robjohn
  • 353,833
0

$\textbf{Proof of 3 :}$

Name the circles as in problem $2$. Let $O_i$ be a center of $i-th$ circle. Easy to check that $O_7, O_8, O_9, O_{10}$ lie on the ellipse with focuses $O_4, O_3$. Similarly draw other ellipses. Now problem follows from problem $11.17$ from https://www.mccme.ru/~akopyan/papers/EnGeoFigures.pdf

$\textbf{The second proof of 3:}$

Name the circles as in problem $2$.

Consider stereographic projection $\pi$. Let the circle $i'$ is the image of the circle $i$ under $\pi$. Let the planes which contain the circles $7', 8'$ meet on the line $\ell_1$ in $3D$ space. Similarly define $\ell_2, \ell_3$.

Now note that projection of the polar line of $\ell_1$ wrt the sphere under $\pi$ on plane is a line joining the centers of $7, 8$. So it's enough to prove that the lines $\ell_1, \ell_2, \ell_3$ lie on the same plane.

But now we can take other stereographic projections $\pi_I$ of the sphere with circles $i'$ on it. And it means that we can use inversions in original problem, and only need to prove it for any $3$ different inversion images of the circles $i$.

solver6
  • 141