How to solve harmonic oscillator differential equation: $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$

Question

I am able to solve simple differential equations like :

$$\dfrac{dy}{dx} = 3x^2 + 2x$$

We simply bring $dx$ to other site and integrate.

But how do we find solutions of differential equations like :

$$\frac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$$

?

We have been told the solution is $x(t) = A\cos ( \omega t + \phi_o)$ where $\omega\ =\sqrt{\dfrac{k}{m}}$

but how do we actually find it?

Answer 1

For convenience, $$x''+\omega^2x=0.$$

Solution 1:

Multiply by $2x'$, to get

$$2x'x''+2\omega^2xx'=0=(x'^2+\omega^2x^2)'.$$

After integration we get a separable equation

$$x'^2+\omega^2x^2=C^2,$$ or $$\frac{x'}{\sqrt{A^2-x^2}}=\omega.$$

Integrating,

$$\arcsin\left(\frac x{A}\right)=\omega t+\phi.$$

---

Solution 2:

Let $D$ denote the differentiation operator. We can rewrite the equation as

$$(D^2+\omega^2)x=0$$ and factor

$$(D-i\omega)(D+i\omega)x=0.$$

Indeed, $(D-i\omega)(D+i\omega)x=(D-i\omega)(x'+i\omega x)=x''+i\omega x'-i\omega(x'+i\omega x)=x''+\omega^2x$.

If we define $y=(D+i\omega)x$, we need to solve

$$(D-i\omega)y=0,$$ i.e.

$$\frac{y'}y=i\omega.$$

The solution is easily found to be

$$y=Ce^{i\omega t}.$$

Now we need to solve

$$(D+i\omega)x=y=Ce^{i\omega t}.$$

The solution is found by combining the general solution of the homogenous equation, $C'e^{-i\omega t}$, found similarly, and a particular solution of the non-homogeneous equation.

When trying $y=C''e^{i\omega t}$, we have

$$C''i\omega e^{i\omega t}+C''i\omega e^{i\omega t}=Ce^{i\omega t}$$ which is a valid solution.

Then

$$x=C'e^{-i\omega t}+C''e^{i\omega t}.$$

As the solution must be real, it can be rewritten as

$$x=C'\cos(\omega t)+C''\sin(\omega t)=A\sin(\omega t +\phi).$$

---

Solution 3:

We recall that $(\sin(t))''=-\sin(t)$ and $(\cos(t))''=-\cos(t)$.

Then scaling with the coefficient $\omega$, $(\sin(\omega t))''=-\omega^2\sin(\omega t)$ and $(\cos(\omega t))''=-\omega^2\cos(\omega t)$.

These are two independent solutions of the differential equation, and as the equation is of the second order, the linear combination of these two functions is the general solution

$$x=C\cos(\omega t)+S\sin(\omega t).$$

---

Solution 4:

The characteristic equation is $\lambda^2+\omega^2=0$ and has the solutions $\lambda=\pm i\omega$. Hence the general solution

$$C_+e^{i\omega t}+C_-e^{-i\omega t}.$$

As we want a real solution, after expansion and cancelling of the imaginary part,

$$x=C\cos\omega t+S\sin\omega t.$$

---

Solution 5:

The equation is autonomous (no explicit appearance of time).

Let $v:=x'$. We have $x''=\dfrac{dv}{dt}=\dfrac{dv}{dx}\dfrac{dx}{dt}=v\dfrac{dv}{dx}$. The equation turns to

$$v\frac{dv}{dx}+\omega^2 x=0$$ or $$v^2+\omega^2 x^2=C$$ and we join the solution 1.

---

Solution 6:

Let us try the entire series $\displaystyle\sum_{n=0}^\infty a_nt^n$.

We get

$$\sum_{n=2}^\infty (n(n-1)a_nt^{n-2}+\omega^2a_nt^n)=0,$$

giving the recurrence

$$a_{n+2}=-\frac{\omega^2a_n}{(n+1)(n+2)}$$ and $a_0,a_1$ are free.

Hence,

$$x=a_0\sum_{n=0}^\infty(-\omega^2)^n\frac{t^{2n}}{(2n)!}+a_1\sum_{n=0}^\infty(-\omega^2)^n\frac{t^{2n+1}}{(2n+1)!}.$$

We recognize $a_0\cos(\omega t)+\dfrac{a_1}\omega\sin(\omega t)$.

---

Solution 7:

Let us try and find the Taylor development of $x$ around $t=0$. We have no information on $x_0:=x(0)$ nor $x'_0=x'(0)$, which are free parameters. Then

$$x''(0)=-\omega^2x(0)=-\omega^2x_0,\\ x'''(0)=-\omega^2x'(0)=-\omega^2x'_0,\\ x''''(0)=-\omega^2x''(0)=\omega^4x_0,\\ x'''''(0)=-\omega^2x'''(0)=\omega^4x'_0,\\ \cdots$$

Hence by induction,

$$x^{(2n)}(0)=(-\omega^2)^nx_0,\\x^{(2n+1)}(0)=(-\omega^2)^nx'_0.$$

Finally, in a way similar to solution 6, $x(t)=x_0\cos(\omega t)+\dfrac{x'_0}\omega\sin(\omega t)$.

---

Solution 8:

Let us rewrite the second order ODE as a system of the first order,

$$\begin{cases}x'=y,\\y'=-\omega^2x,\end{cases}.$$

In matrix form

$$\begin{pmatrix}x'\\y'\end{pmatrix}=\begin{bmatrix}0&1\\-\omega^2&0\end{bmatrix}\begin{pmatrix}x\\y\end{pmatrix}.$$

We know that the solution of such a system is obtained from the exponential of the matrix, itself a function of its Eigenvalues. The Eigenvalues are $\pm i\omega$ and the solution will be of the form

$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{bmatrix}e^{i\omega}&0\\0&e^{-i\omega}\end{bmatrix}\begin{pmatrix}a\\b\end{pmatrix}.$$

For a real solution, we must have $b=a^*$.

Alternatively, we can compute the powers of the matrix, let $M$. We observe that

$$M^2=\begin{bmatrix}0&1\\-\omega^2&0\end{bmatrix}\begin{bmatrix}0&1\\-\omega^2&0\end{bmatrix}=\begin{bmatrix}-\omega^2&0\\0&-\omega^2\end{bmatrix}=-\omega^2I.$$

Hence the powers are alternatively $(-\omega^2)^{2n}I$ and $(-\omega^2)^{2n}M$, and we obtain the exponential as

$$\sum_{n=0}^\infty M^n\begin{pmatrix}x_0\\y_0\end{pmatrix}\frac{t^k}{k!}=\left(I\cos(\omega t)+M\frac{\sin(\omega t)}{\omega}\right)\begin{pmatrix}x_0\\y_0\end{pmatrix}.$$

---

Solution 9:

By Laplace,

$$\mathcal L(x''+\omega x)=s^2\mathcal Lx-sx_0-x'_0+\omega^2\mathcal Lx=0$$

and

$$\mathcal Lx=\frac{sx_0+x'_0}{s^2+\omega^2}.$$

Reverting to the original by means of a table,

$$x(t)=x_0\cos(\omega t)+\frac{x'_0}{\omega}\sin(\omega t).$$

The resolution by the Fourier transform is uneasy as it requires the use of distributions.

---

Solution 10:

We can integrate the equation numerically, for instance with a Runge-Kutta solver. But we have a dependency on three parameters, namely $\omega$ and the initial conditions $x(0),x'(0)$.

We can remove the first dependency by rescaling time, let $\tau:=\omega t$, giving

$$\ddot x+x=0.$$

Accordingly, we update the initial condition $\dot x(0)=\dfrac{x'(0)}{\omega}$. To remove the dependency on the initial conditions, we observe that the equation is (luckily) linear and it suffices to solve for the two canonical cases $x(0)=1,\dot x(0)=0$ and $x(0)=0,\dot x(0)=1$.

Here is a plot of the results of integration:

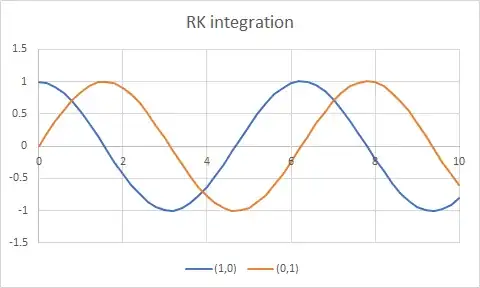
Now the general solution is a linear combination of these two canonical functions, that can be tabulated once for all.

---

Solution 11:

By Picard's method, we start with a linear solution that satisfies the initial conditions

$$z_0(t)=x'_0t+x_0.$$

Then we integrate $x''=-\omega^2x$ twice and still fulfilling the initial conditions, get

$$z_1(t)=x'_0t+x_0-\omega^2\int_0^t\int_0^t(x'_0t+x_0)dt=x'_0t+x_0-\omega^2\frac{t^3}{3!}x'_0-\omega^2\frac{t^2}2.$$

The next step yields

$$z_2(t)=x'_0t+x_0-\omega^2\frac{t^3}{3!}x'_0-\omega^2\frac{t^2}2+\omega^4\frac{t^5}{5!}x'_0-\omega^4\frac{t^4}{4!}$$

and one recognizes the pattern for the sine and cosine developments.

Answer 2

HINT:

$$x''(t)+\frac{kx(t)}{m}=0\Longleftrightarrow$$ $$\frac{\text{d}^2x(t)}{\text{d}t^2}+\frac{kx(t)}{m}=0\Longleftrightarrow$$

---

Assume a solution will be proportional to $e^{\lambda t}$ for some constant $\lambda$.

Substitute $x(t)=e^{\lambda t}$ into the differential equation:

---

$$\frac{\text{d}^2}{\text{d}t^2}\left(e^{\lambda t}\right)+\frac{ke^{\lambda t}}{m}=0\Longleftrightarrow$$

---

Substitute $\frac{\text{d}^2}{\text{d}t^2}\left(e^{\lambda t}\right)=\lambda^2e^{\lambda t}$:

---

$$\lambda^2e^{\lambda t}+\frac{ke^{\lambda t}}{m}=0\Longleftrightarrow$$ $$e^{\lambda t}\left(\lambda^2+\frac{k}{m}\right)=0\Longleftrightarrow$$

---

Since $e^{\lambda t}\ne 0$ for any finite $\lambda$, the zeros must come from the polynomial:

---

$$\lambda^2+\frac{k}{m}=0\Longleftrightarrow$$ $$\frac{k+m\lambda^2}{m}=0\Longleftrightarrow$$ $$\lambda=\pm\frac{i\sqrt{k}}{\sqrt{m}}$$

Answer 3

Basically, you are solving $\ddot{x}=-\omega_0^2x$. Double dot over $x$ means double derivative wrt time $t$. This is easily seen to be equivalent to $$\Big(\frac{d}{dt}+i\omega_0\Big)\Big(\frac{d}{dt}-i\omega_0\Big)x=0.$$ This would imply $$\Big(\frac{d}{dt}-i\omega_0\Big)x= const$$ You can take it from here using the method you use by transferring $dt$ on the other side and integrating.

Answer 4

The equation:

$y'' = -k^2 \cdot y$

Has the completesolution:

$y = f(x) = c_1 \cos(kx) + c_2 \sin(kx)$

Proof:

First we define two function g(x) and h(x)

$g(x)=f(x)\cos(kx)-\frac{1}{k}f'(x)\sin(kx)$

$h(x) = f(x)\sin(kx)+\frac{1}{k}f'(x)\cos(kx)$

We differentiate g(x) and h(x): (Using the product and chain rule)

$g'(x)=f'(x)\cos(kx)-f(x)k\sin(kx)-\frac{1}{k}(f''(x)\sin(kx)+f'(x)k\cos(kx))$

$h'(x)=f'(x)\sin(kx)+f(x)k\cos(kx)+\frac{1}{k}(f''(x)\cos(kx)-f'(x)k\sin(kx))$

Now comes the critical point. Lets assume the function f(x) is a solution to the differentialequation. If and only if f(x) is a solution the we can write:

$f''(x)=-k^2f(x)$

We can use this in the g(x) and h(x) functions and substitute for f''(x) and reduce the expression:

$g'(x)=f'(x)\cos(kx)-f(x)k\sin(kx)-\frac{1}{k}(\color{red}{-k^2f(x)}\sin(kx)+f'(x)k\cos(kx)) \Leftrightarrow$

$g'(x)=0$

$h'(x)=f'(x)\sin(kx)+f(x)k\cos(kx)+\frac{1}{k}(\color{red}{-k^2f(x)}\cos(kx)-f'(x)k\sin(kx)) \Leftrightarrow$

$h'(x)=0$

When the derivative of the functions are 0, then the functions themself must be constants:

$g(x)=c_1 \;\;\;$ and $\;\;\;h(x)=c_2$

So we insert this in the two first equations:

$c_1=f(x)\cos(kx)-\frac{1}{k}f'(x)\sin(kx)$

$c_2 = f(x)\sin(kx)+\frac{1}{k}f'(x)\cos(kx)$

We multiply the $c_1$ equation with cos(kx) and we multiply the $c_2$ equation with sin(kx):

$c_1 \cos(kx)=f(x)\cos(kx)^2-\frac{1}{k}f'(x)\sin(kx)\cos(kx)$

$c_2 \sin(kx) = f(x)\sin(kx)^2+\frac{1}{k}f'(x)\cos(kx)\sin(kx)$

We then add the two equations:

$c_1 \cos(kx) + c_2 \sin(kx) = f(x)\cos(kx)^2-\frac{1}{k}f'(x)\sin(kx)\cos(kx) + f(x)\sin(kx)^2+\frac{1}{k}f'(x)\cos(kx)\sin(kx) \Leftrightarrow$

$c_1 \cos(kx) + c_2 \sin(kx) = f(x)\cos(kx)^2 + f(x)\sin(kx)^2 \Leftrightarrow$

$c_1 \cos(kx) + c_2 \sin(kx) = f(x)(\cos(kx)^2 + \sin(kx)^2) \Leftrightarrow$

$c_1 \cos(kx) + c_2 \sin(kx) = f(x)(1) \Leftrightarrow$

$c_1 \cos(kx) + c_2 \sin(kx) = f(x)$

All that is left is to test if this is a solutions by inserting in the differential equation. If you do that, you will find it is a solution.

Q.E.D