How to Evaluate $\int_0^1 {\frac{{u\arcsin u}}{{{u^4} + 2{u^2} + 13}}du} .$?

Question

How to find $$\int_0^1 {\frac{{u\arcsin u}}{{{u^4} + 2{u^2} + 13}}du} .$$

In fact, \begin{align*} &\int_0^1 {\frac{{u\arcsin u}}{{{u^4} + 2{u^2} + 13}}du} \\ =& \int_0^1 {\frac{{u\arcsin u}}{{\left( {{u^2} - \sqrt {2\sqrt {13} - 2} u + \sqrt {13} } \right)\left( {{u^2} + \sqrt {2\sqrt {13} - 2} u + \sqrt {13} } \right)}}du} \\ = &\frac{1}{{2\sqrt {2\sqrt {13} - 2} }}\left[ {\int_0^1 {\frac{{\arcsin u}}{{{u^2} - \sqrt {2\sqrt {13} - 2} u + \sqrt {13} }}du} - \int_0^1 {\frac{{\arcsin u}}{{{u^2} + \sqrt {2\sqrt {13} - 2} u + \sqrt {13} }}du} } \right]. \end{align*}

But how can we continue?

Answer 1

Rewrite $\arcsin u = \arctan \dfrac u{\sqrt{1-u^2}} = \arctan v$:

$$\begin{align*} I &= \int_0^1 \frac{u \arcsin u}{u^4 + 2u^2 + 13} \, du \\ &= \int_0^1 \frac{u \arctan \frac u{\sqrt{1-u^2}}}{u^4 + 2u^2 + 13} \, du \\ &= \int_0^\infty \frac{\frac v{\sqrt{1+v^2}} \arctan v}{\frac{v^4}{\left(1+v^2\right)^2} + \frac{2v^2}{1+v^2} + 13} \, \frac{dv}{\left(1+v^2\right)^{3/2}} \\ &= \int_0^\infty \frac{v \arctan v}{16v^4 + 28v^2 + 13} \, dv \\ &= \frac12 \int_{-\infty}^\infty \frac{v \arctan v}{16v^4 + 28v^2 + 13} \, dv \end{align*}$$

Now integrate the complex function,

$$f(z) = \frac{z \arctan z}{16z^4 + 28z^2 + 13} = -\frac i2 \frac{z}{16z^4 + 28z^2 + 13} \left(\log\left\lvert\frac{i-z}{i+z}\right\rvert + i \arg\left(\frac{i-z}{i+z}\right)\right)$$

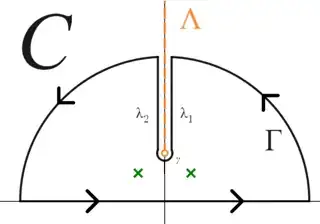
along an indented semicircular contour $C$ (a modified reproduction of the contour provided in @Accelerator's answer here), avoiding a branch cut taken along $i[1,\infty)$ and enclosing the poles $\omega_1=\color{red}-\dfrac{\sqrt{-7\color{red}-i\sqrt3}}{2\sqrt2}$ and $\omega_2=\color{red}+\dfrac{\sqrt{-7\color{red}+i\sqrt3}}{2\sqrt2}$, indicated approximately by the green X marks. (I use the branch of $\sqrt z$ with $\arg z\in(-\pi,\pi)$.)

By the residue theorem, and taking a shortcut with Mathematica to simplify the RHS as much as possible,

$$\oint_C f(z) \, dz = i2\pi \sum_{\omega_1,\omega_2} \operatorname{Res} f(z) = \frac{\pi^2}{8\sqrt3} - \frac\pi{8\sqrt3} \arctan \left(\frac4{79} \sqrt{21+114\sqrt{13}}\right)$$

The integrals along the circular arcs $\Gamma$ and $\gamma$ will vanish as their respective radii get arbitrarily large/small. As the paths $\lambda_1,\lambda_2$ approach the cut from either side, we have

$$\begin{align*} \int_{\lambda_1} f(z) \, dz &= \int_R^{1+\varepsilon} f(\varepsilon+iy) \cdot i\,dy \\ &\to -\frac i2 \int_1^\infty \frac{y}{16y^4 - 28y^2 + 13} \left(\log\left(\frac{y-1}{y+1}\right) + i \pi\right) \, dy \\[2ex] \int_{\lambda_2} f(z) \, dz &= \int_{1+\varepsilon}^R f(-\varepsilon+iy) \cdot i\,dy \\ &\to \frac i2 \int_1^\infty \frac{y}{16y^4 - 28y^2 + 13} \left(\log\left(\frac{y-1}{y+1}\right) - i \pi\right) \, dy \\[2ex] \implies \int_{\lambda_1\cup\lambda_2} f(z)\,dz &= \pi \int_1^\infty \frac{y}{16y^4 - 28y^2 + 13} \, dy \\ &= \pi \int_1^\infty \frac{y}{16 \left(y^2 - \frac78\right)^2 + \frac{3}{4}} \, dy = \frac{\pi^2}{12\sqrt3} \end{align*}$$

It follows that

$$\int_{-\infty}^\infty f(v) \, dv = \frac{\pi^2}{24\sqrt3} - \frac\pi{8\sqrt3} \arctan \left(\frac4{79} \sqrt{21+114\sqrt{13}}\right) \\ \implies I = \boxed{\frac{\pi^2}{48\sqrt3} - \frac\pi{16\sqrt3} \arctan \left(\frac4{79} \sqrt{21+114\sqrt{13}}\right)}$$

Answer 2

Integrate by parts, followed by $u=\sin t$ \begin{align} &\int_0^1 {\frac{{u\arcsin u}}{{{u^4} + 2{u^2} + 13}}du}\\ =&\ \frac1{4\sqrt3}\bigg[ \frac{\pi^2}{12}-\int_0^{\pi/2}\tan^{-1}\left(\frac1{\sqrt3}\sin^2t + \frac1{2\sqrt3}\cos^2t \right)dt\bigg]\\ = &\ \frac\pi{4\sqrt3}\bigg( \frac{\pi}{12}-\tan^{-1}\frac{\sqrt{1+\sqrt{13}}-\sqrt2}{\sqrt{1+\sqrt{13}}+\sqrt2}\bigg) \end{align} where $\int_0^{\pi/2}\tan^{-1}\left(\sinh a\sin^2t + \sinh b\cos^2t \right)dt = \pi \tan^{-1}\left( \tanh\frac{a+b}4\right)$.

Answer 3

Thanks to the top answer $$I=\int_0^1\frac{x\arcsin x}{x^4+2x^2+13}dx=\int_0^\infty \frac{x\arctan x}{16x^4+28x^2+13}dx$$ Use an integral representation of $\arctan x$ and switch order of integration $$I=\int_0^1\int_0^\infty \frac{x^2}{(16x^4+28x^2+13)(x^2y^2+1)}dx\space dy$$ Use partial fractions $$I=\int_0^1\int_0^\infty\left(\frac{16x^2+13y^2}{(13y^4-28y^2+16)(16x^4+28x^2+13)}-\frac{y^2}{(13y^4-28y^2+16)(x^2y^2+1)}\right)dx\space dy$$ $$=\left(\int_0^\infty \frac{16x^2dx}{16x^4+28x^2+13}\right)\left(\int_0^1 \frac{dy}{13y^4-28y^2+16}\right)+\left(\int_0^\infty \frac{dx}{16x^4+28x^2+16}\right)\left(\int_0^1 \frac{13y^2dy}{13y^4-28y^2+16}\right)-\frac{\pi}{4}\int_0^1\frac{\space dy}{13y^2-28y+16}$$ We are left with a few integrals that are trivial, but tedious to evaluate

Answer 4

From user170231's answer, one has $$ I =\int_0^1 {\frac{{u\arcsin u}}{{{u^4} + 2{u^2} + 13}}du} =\int_0^\infty \frac{x\arctan (x)}{16x^4+28x^2+13}dx.$$ Let $$I(a)=\int_0^\infty \frac{x\arctan (ax)}{16x^4+28x^2+13}dx$$ and then $$I'(a)=\int_0^\infty \frac{x^2}{(1+a^2x^2)(16x^4+28x^2+13)}dx.$$ Let $$ 16x^4+28x^2+13=16(x^2+b^2)(x^2+c^2)$$ where $$ b^2=\frac18(7 + i\sqrt{3}), c^2=\frac18(7 - i\sqrt{3}).$$ Then $$I'(a)=\frac1{16}\int_0^\infty \frac{x^2}{(1+a^2x^2)(x^2+b^2)(x^2+c^2)}dx=\frac{\pi}{32(b + c) (1 + a b)(1 + a c)}.$$ So $$ I=\frac1{32}\int_0^1 \frac{π}{(b + c)(1 + a b)(1 + a c)}da=\frac{\pi(\log(1 + b) - \log(1 + c)))}{32 (b^2 - c^2)}=\frac{\pi}{32\sqrt3i}\bigg(\log\left(1+\sqrt{\frac18(7 + i\sqrt{3})}\right)-\log\left(1+\sqrt{\frac18(7 - i\sqrt{3})}\right)\bigg).$$ A tedious simplification of the above will give the answer.

Answer 5

by putting $u=\frac{x}{\sqrt{x^2+1}}$ we have $$I=\int_0^1 \frac{u\sin^{-1}u}{u^4+2u^2+13} du=\int_0^{\infty} \frac{x\tan^{-1}x}{16x^4+28x^2+13} dx $$ where $\sin^{-1}u=\tan^{-1}x$ and now by using integral by part where $$ du=\frac{x}{16x^4+28x^2+13} dx \to u=\frac{1}{4\sqrt{3}} \tan^{-1} \left(\frac{8}{\sqrt{3}} x^2 + \frac{7}{\sqrt{3}}\right)$$ therefore $$ I=\frac{\pi^2}{16\sqrt{3}}-\frac{1}{4\sqrt{3}} \int_0^\infty \frac{1}{x^2+1} \tan^{-1} \left(\frac{8}{\sqrt{3}} x^2 + \frac{7}{\sqrt{3}}\right) dx $$ we can prove that for real number $a,b$ $$ \int_0^\infty \frac{\tan^{-1} \left(ax^2+b\right)}{x^2+1} dx=\pi \arg(\sqrt{ai}+\sqrt{1+bi})$$ So

$$ I=\frac{\pi^2}{16\sqrt{3}}-\frac{\pi}{4\sqrt{3}} \arg\left(\sqrt{\frac{8}{\sqrt{3}}i}+\sqrt{1+\frac{7}{\sqrt{3}}i}\right) $$ but $$ \arg\left(\sqrt{\frac{8}{\sqrt{3}}i}+\sqrt{1+\frac{7}{\sqrt{3}}i}\right)=\tan^{-1} \left(\frac{4+\sqrt{2} \sqrt[4]{55-4\sqrt{39}}}{4+\sqrt{2} \sqrt[4]{55+4\sqrt{39}}} \right)$$ So $$ \int_0^1 \frac{u\sin^{-1}u}{u^4+2u^2+13} du=\frac{\pi^2}{16\sqrt{3}}-\frac{\pi}{4\sqrt{3}} \tan^{-1} \left(\frac{4+\sqrt{2} \sqrt[4]{55-4\sqrt{39}}}{4+\sqrt{2} \sqrt[4]{55+4\sqrt{39}}} \right)\approx 0.026783223 $$

Answer 6

This is probably not an answer

Being too lazy to attack such monsters, I should use Taylor series $$\sin^{-1}(u)=\sum_ 0^\infty\frac{(2n)!}{4^n(n!)^2(2n+1)}u^{2n+1}\qquad (|u|\leq 1)$$ and perform the long division by the denominator. This would lead to $$\frac{{u\sin^{-1} u}}{{{u^4} + 2{u^2} + 13}}=\frac{u^2}{13}+\frac{u^4}{1014}-\frac{79 u^6}{263640}+O\left(u^7\right)$$ If you are brave enough, take more terms !