2

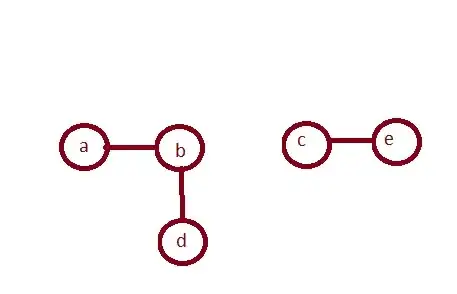
suppose that I have the following undirected graph enter image description here

with the following adjacency matrix showing if there is an edge between the nodes: \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 \end{bmatrix}

Now from the above matrix, I want to find the following matrix which shows if there is a path between each node:

\begin{bmatrix} 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 \end{bmatrix}

We can find the second matrix by checking each node one by one (using transitivity rule) My question is if there is an algorithm for finding the second matrix faster. The matrix I am working with is a huge matrix and I am looking for a good way to implement an algorithm to find the second matrix. In other words I am looking for connected components of the graph. I searched and found that one way is to use Laplacian matrix. For example, for the above example Laplacian matrix would be
\begin{bmatrix} 1 & -1 & 0 & 0 & 0 \\ -1 & 2 & 0 & -1 & 0\\ 0 & 0 & 1 & 0 & -1\\ 0 & -1 & 0 & 1 & 0\\ 0 & 0 & -1 & 0 & 1 \end{bmatrix}

Now using this matrix how can I find the connected components? Is there a fastest way to find the connected components?

May
  • 1,254
  • @amd thank you, my math background is not very strong, how can I find the connected components using laplaccian matrix? I am also looking for other possible solutions. – May Nov 30 '15 at 18:21
  • @hardmath thank you for your comment, I edited the question. – May Nov 30 '15 at 18:28
  • As I note in this previous Answer about the graph-laplacian, the multiplicity of the zero eigenvalue gives the number of connected components in a graph. This can be determined using exact arithmetic in polynomial time (find the rank of the Laplacian matrix), and if you are careful in choosing a basis for the nullspace, you get the individual components. – hardmath Nov 30 '15 at 18:29
  • @hardmath I do not have strong background in linear algebra. Would you please explain a little more? How can I find the components of the above simple example? (not just the number of componets) – May Nov 30 '15 at 18:32
  • Can you put the Laplacian matrix into reduced row-echelon form, e.g. using elementary row operations? – hardmath Nov 30 '15 at 18:33
  • @hardmath no but I used http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=ref to find the reduced row-echelon form of the laplacian matrix in the example: \begin{bmatrix} 1 & -1 & 0 & 0 & 0 \ 0 & 1& 0 & -1 & 0\ 0 & 0 & 1& 0 & -1\ 0 & 0 & 0 & 0 & 0\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} how can I use this to find the components? – May Nov 30 '15 at 18:41
  • You say you’re looking for the fastest algorithm. Before you go too far down this Laplacian path, it might be good to figure out the computational complexity of a straightforward walk of the graph. I suspect that matrix operations are going to be more expensive than that. – amd Nov 30 '15 at 18:50
  • 1
    @hardmath you mean the following? \begin{bmatrix} 1 & 0 & 0 & -1 & 0 \ 0 & 1& 0 & -1 & 0\ 0 & 0 & 1 & 0 & -1\ 0 & 0 & 0 & 0 & 0\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} how does it show the components? – May Nov 30 '15 at 18:57
  • @amd yes you are right! I am curious to know how the matrix-based solution work. I am also looking for faster algorithms. – May Nov 30 '15 at 18:59
  • 1
    You can basically read off the kernel once you have the rref form of the matrix. An simple internet search will give you dozens of links on how to do this. The important point is that in this case it will consist of occupancy vectors that represent the components of the graph. – amd Nov 30 '15 at 19:04

1 Answers1

1

Putting the Laplacian matrix into reduced row-echelon form:

$$ \begin{bmatrix} 1 & 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 1& 0 & -1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$

allows us to determine the connected components. Take the columns not containing leading ones, and for each of these set the corresponding variable to $1$ and other such variables to zero. For example, setting the variable from the fourth column to $1$ and the variable from the fifth column to zero gives a solution:

$$ \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} $$

which gives the connected component $\{a,b,d\}$ containing the node $d$ corresponding to that fourth column.

Setting the variable corresponding to the fifth column to $1$ and the variable corresponding to the fourth column to zero gives a different solution:

$$ \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 1 \end{bmatrix} $$

which indicates the connected component $\{c,e\}$ containing the node $e$ corresponding to that fifth column.

As @amd suggests in a Comment on the Question, the well-known algorithm (already per Hopcraft and Tarjan, 1973) for finding all connected components (by searching from each not-yet reached vertex for all its reachable nodes) has complexity $O(|V| + |E|)$ where $V$ is the set of vertices and $E$ the set of edges. This gives at worst $O(|V|^2)$ since $|E| \le |V|(|V|-1)/2$.

Any approach based on the $|V|\times |V|$ matrix (whether adjacency or graph-Laplacian) cannot improve on that asymptotically, because scanning such a matrix already takes $O(|V|^2)$ steps. Indeed row-reducing a general $|V|\times |V|$ matrix has $O(|V|^3)$ complexity.

See an earlier SO Question for a discussion of the "path matrix" (as mentioned by amd in a Comment on this answer):

What does it mean by “Path Matrix” and “Transitive Closure” of a graph?

Community
  • 1
hardmath
  • 37,715
  • 1
    If you let $B$ be the matrix with these basis vectors as its columns, then $BB^T-I$ is the desired path matrix. – amd Dec 01 '15 at 04:08