2

Consider the boundary value problem $$\varepsilon \frac{d^2y}{dx^2}+(1+x)\frac{dy}{dx}+y=0$$ subject to $y(0)=0$, $y(1)=1$, for $0 \leq x \leq 1$.

By considering the rescaling $x=x_0+\varepsilon ^{\alpha} X$ and $y=Y$,

for $X,Y=O(1)$ and $\alpha >1$, show that a boundary layer is only possible at $x=0$

So after rescaling, we have $$\varepsilon \frac{d^2y}{dx^2}+(1+x_0+\varepsilon ^{\alpha} X)\frac{dy}{dx}+Y=0$$

At leading order (when $\varepsilon =0$): $$(1+x_0+\varepsilon ^{\alpha} X)\frac{dy}{dx}+Y=0$$ which gives $$Y(1+x_0+\varepsilon ^{\alpha} X)=\frac{A_0}{1+x_0+\varepsilon ^{\alpha} X}$$

We have two boundary conditions. When $y(0)=0$ confuses me because then there would be a zero divider (so that must mean $y$ changes rapidly right?)

So what exactly do we do next to answer the question...

snowman
  • 3,799
  • 8
  • 44
  • 78
  • I can't write up an answer now, but take a look at the process in this answer, as well as the comments beneath it. – Antonio Vargas Nov 18 '15 at 00:40
  • @AntonioVargas Just had a look. It's quite confusing... In lectures they seemed to consider when epsilon is $0$ but in the link, it seems different. I think I might be misunderstanding. If you get time, please would you write something up. – snowman Nov 18 '15 at 00:44

1 Answers1

5

You rescaled equation is incorrect, derivatives with respect to $x$ must also be transformed into derivative with respect to $X$. The easiest way to do this is with the chain rule, $$ \frac{dy}{dx}=\frac{dy}{dX}\frac{dX}{dx}=\epsilon^{-\alpha}\frac{dy}{dX}. $$

So your rescaled equation is $$\epsilon^{1-2\alpha}\frac{d^2Y}{dX^2}+(1+x_0+\epsilon^{\alpha}X)\epsilon^{-\alpha}\frac{dY}{dX}+Y=0, $$ or, separating powers of $\epsilon$, $$\epsilon^{1-2\alpha}\frac{d^2Y}{dX^2}+(1+x_0)\epsilon^{-\alpha}\frac{dY}{dX}+X\frac{dY}{dX}+Y=0. $$ Now, the $XY'(X)$ and $Y$ terms will be smaller than the $\epsilon^{1-2\alpha}$ and $\epsilon^{-\alpha}$ terms, so we need to balance $-\alpha$ and $1-2\alpha$, which means $\alpha=1$, and our leading order equation is $$ \frac{d^2Y}{dX^2}+(1+x_0)\frac{dY}{dX}=0. $$ The solution is $$Y=A\exp(-(1+x_0)X)+B$$ (this is the inner solution, or boundary layer solution). Now the inner solution should cannot grow exponentially out of a boundary layer, as if it did, you couldn't match it to the outer solution. This means you need the argument of $\exp$ ($-(1+x_0)X$) to be negative as $X$ goes out of the layer. If the layer is internal, you need $-(1+x_0)X=0$ as $|X|\rightarrow\infty$, if the layer is at the left end, you need $-(1+x_0)X<0$ as $X\rightarrow\infty$ and if the layer is at the right end of the interval, you need $-(1+x_0)X<0$ as $X\rightarrow-\infty$. Since $1+x_0\geq1$ we can only have a layer at the left end $x=0$.

The outer solution is what you get for $\epsilon=0$ in the unscaled equation, $$(1+x)\frac{dy}{dx}+y=\frac{d}{dx}\left((1+x)y\right)=0,$$ so $y=C/(x+1)$. If the boundary layer is at $x=0$ then the outer boundary condition is $y(1)=1$ so $C=2$.

To close the system you have to use matching conditions, $$\lim_{X\rightarrow\infty}Y(X)=\lim_{x\rightarrow0}y(x) $$ which gives $$\lim_{X\rightarrow\infty} A\left(e^{-X}-1\right)=2 $$ so $A=-2$ and $Y(X)=-2(e^{-X}+1)$. (Think about what would happen if we had $e^X$ instead of $e^{-X}$, this is why the layer had to be at $x=0$.)

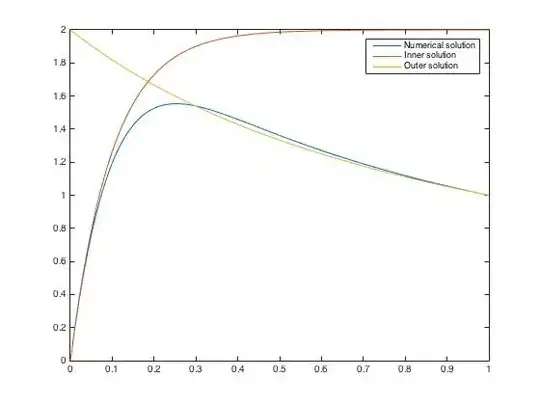
And because they are always cool, here's the picture you get, for $\epsilon=0.1$, just to make sure. enter image description here

David
  • 2,514
  • Nice exposition, especially the part about determining $x_0$. – Antonio Vargas Nov 18 '15 at 13:23
  • @David How did you get to $1+x_0 \geq 1$, how do you know that $x_0$ is nonnegative? – snowman Nov 18 '15 at 20:07
  • Because your domain is $0\leq x\leq 1$, if you have a boundary layer anywhere, it is between ) and 1, so $0\leq x_0\leq 1$. @AntonioVargas thanks, I think it's the first time I've really understood it properly myself, it was a good exercise to go through! – David Nov 18 '15 at 21:35
  • @David Thanks. There is a next part of the q which is: Use the method of matched asymptotic expansions to construct two-term inner and outer expansions to the problem, which should then be matched using Van Dyke's matching principle. The inner solution would be in terms of $x$ and $y$, $$y=B+Ae^{-\frac{x-x_0}{\varepsilon}}$$ but as epsilon tends to zero, it is $y=B$ right? – snowman Nov 19 '15 at 22:42
  • I got the outer solution as $$y=2(1+x)^{-1}+\varepsilon \bigg(\frac43(1+x)^{-4}-\frac16(1+x)^{-1} \bigg)$$ and this as terms of $X$ and $Y$ is $$Y=2(1+x_0+\varepsilon X)+\varepsilon \bigg(\frac43(1+x_0+\varepsilon X)^{-4}-\frac16(1+x_0 +\varepsilon X)^{-1} \bigg) +O(\varepsilon ^2)$$ and when you match these you get $B=2+2x_0$ right? Have I done it right? Can I have some help please. – snowman Nov 19 '15 at 22:43