2

We got set some work to find some interesting facts or proofs regarding rational and irrational numbers. I wonder if anyone could offer some insight or recommend a good book/ website to look at.

Tk706
  • 271
  • 2
  • 6
  • 13
  • We don't know whether $e+\pi$ is transcendental over $\mathbb{Q}$ – AnotherPerson Nov 16 '15 at 10:24
  • But we do know that one of $e +\pi$ or $e \pi$ is transcendental – happymath Nov 16 '15 at 10:31
  • thanks do you have any websites that explain this? With proofs and theory? – Tk706 Nov 16 '15 at 10:33
  • 1
    @Tk706 the fact I have written is easy to show if we assume that we know that $e$ is transcendental. Now assuming that if $e+ \pi$ and $e \pi$ were algebraic then the roots of $x^2-(e+ \pi)x+ e \pi=0$ are algebraic, which is a contradiction. – happymath Nov 16 '15 at 10:36
  • A book which might help you is A comprehensive course in Number Theory by Alan Baker. I found it very interesting and it covers continued fractions which can be used to give proofs of irrationality – happymath Nov 16 '15 at 10:38
  • Also you should look up Gelfond Schneider Theorem here – happymath Nov 16 '15 at 10:54
  • @SirJective : It seems that your example cannot be called a 'fact".. –  Nov 16 '15 at 10:55
  • I particularly like the proof that the set of rational numbers is not closed. This property allows the construction of $\mathbb {R} $ from the rationals – Malcolm Nov 16 '15 at 10:58
  • 1
    @JohnMa I think we can call it a fact because statement says We don't know whether $e+ \pi$ is transcendental over Q which if I am not wrong is not really known so is actually a fact – happymath Nov 16 '15 at 10:59
  • @happymath Actually we are talking about algebricity over $\mathbb{Q}$ so I don't understand how the fact that $e+\pi$and $e\pi$ are algebraic imply that the solution of the polynom $x^2-(e+\pi)x+e\pi$ will be algebraic? – EDX Jul 19 '20 at 17:50

2 Answers2

1

You may find the Gelfond-Schneider theorem interesting. The theorem states that:

If $a$ and $b$ are algebraic numbers with $a ≠ 0,1$ and $b$ non-rational, then any value of $a^b$ is a transcendental number.

This not only gives rise to trivial results such that $2^{\sqrt 2}$ is irrational, but to some more interesting ones as well. For instance, by taking $a=-1$ and $b=-i$, where $i=\sqrt {-1}$, we can obtain the following result:

$$ (-1)^{-i} = \left( e^{i \pi} \right)^{-i} = e^\pi, $$

showing that $e^\pi$ is transcendental.

Klangen
  • 5,459
0

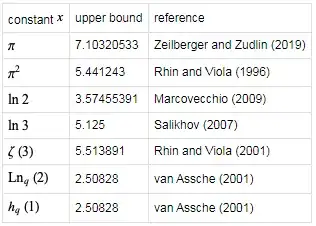
The irrationality measure $\mu(x)$ of numbers such as $x=\pi$ or $x=e$ has been studied in detail, but there are still plenty of conjectures. You can find the definition of this measure, here. In particular:

  • $\mu(x)=1$ if $x$ is rational
  • $\mu(x)=2$ if $x$ is algebraic of degree $> 1$
  • $\mu(x)\geq 2$ if $x$ is transcendental

More results about $\mu(x)$:

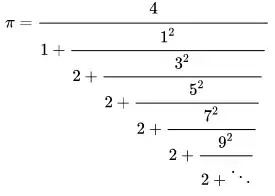
enter image description here

Another topic of interest is non-periodic continued fractions for irrational numbers, for instance (see here):

enter image description here

Another surprising fact is a simple recurrence relation to compute all the digits of some quadratic irrationals (see here) which could potentially help determining whether they are normal numbers:

enter image description here

Resulting in

enter image description here

Here the $d_n$'s are the digits of $x$.

Other results

  • If $x$ and $x'$ are irrational normal numbers linearly independent over the set of rational numbers, then the correlation between the binary digits of $x$ and $x'$ is equal to zero. See here.
  • If $x$ is irrational, then the sequence $\{kx\}$ where $k=0,1,2\cdots$ and the brackets represent the fractional part function, are equidistributed modulo 1.
Vincent Granville
  • 3,759