Is there an intuitive (e.g. graphical) interpretation of the proof that projections on closed convex sets are non-expansive?
Most proofs, e.g. the one given here, are presented as a sequence of algebraic transformations and do not explain what these transformations mean in terms of geometry. This makes them hard to remember.
There are two relevant geometric observations. Consider the following drawing of a quadrilateral with $\theta_1, \theta_2 \geq \frac{\pi}{2}$:
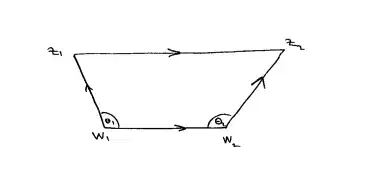
Then $|w_2 - w_1| \leq |z_2 - z_1|$. In order to prove it algebraically, we have
$$ \left< w_2 - w_1, w_2 - w_1 \right> = \left< (z_1 - w_1) + (z_2 - z_1) + (w_2 - z_2), w_2 - w_1 \right> = \\ \left< z_1 - w_1, w_2 - w_1 \right> + \left< z_2 - z_1, w_2 - w_1 \right> + \left< w_2 - z_2, w_2 - w_1 \right>.$$
Since $\theta_1 \geq \frac{\pi}{2}$, we have $\left< z_1 - w_1, w_2 - w_2 \right> \leq 0$. Similarly, since $\theta_2 \geq \frac{\pi}{2}$ we have $$ \left< z_2 - w_2, w_1 - w_2 \right> = \left< w_2 - z_2, w_2 - w_1 \right> \leq 0. $$
Combining the inequalities and using the Cauchy-Schwarz inequality, we see that
$$ |w_2 - w_1|^2 = \left< w_2 - w_1, w_2 - w_1 \right> \leq \left< z_2 - z_1, w_2 - w_1 \right> \leq |z_2 - z_1||w_2 - w_1| $$
showing that $|w_2 - w_1| \leq |z_2 - z_1|$.
Now, to prove that the projection is distance-decreasing, consider the following drawing:
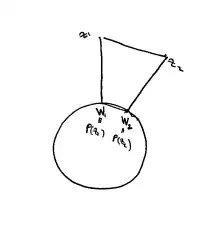
Recall that the projection $P$ satisfies $\left< z - P(z), x - P(z) \right> \leq 0$ for all $x \in C$. This means that the angle between $z - P(z)$ and $x - P(z)$ is greater than or equal to $\frac{\pi}{2}$. Geometrically, $z - P(z)$ lies on one half of the separating half-space at $P(z)$ while $x - P(z)$ lies on the other half. Applying this observation to $z = z_1, x = P(z_2)$ and $z = z_2, x = P(z_1)$, we see that we are in the situation described in the beginning of the answer and so the result follows.
