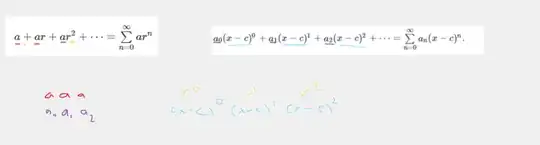9

A geometric series is one having a common ratio, right? Something like:

$$\sum_{n=0}^{\infty} ar^n$$

And a power series is one with the form:

$$\sum_{n=0}^{\infty} c_n(x-a)^n$$

Initially, I thought a geometric power series was one which had a rational function in $x-a$; something like $\frac{x}{2}$ with $a=0$, or maybe $\frac{x-a}{n}$.

But, you can think of the expression $(x-a)$ as a rational function of the form:

$$\frac{(x-a)}{1}$$

So, does that mean all power series (for $x$ within a radius of convergence) are geometric series? It seems so, but I don't want any misconceptions in my understanding, so I thought it best to ask.

tommytwoeyes
  • 719
  • 2
  • 10
  • 16
  • 4
    Your formula for geometric series is wrong. Should have constant coefficient. – ziggurism Nov 10 '15 at 21:53
  • No this is not true, only if your coefficients $c_n$ are constant. – MrMazgari Nov 10 '15 at 21:54
  • 1
    @ziggurism You're right. I fixed it. Sorry, I've been struggling with series so much in the past couple of weeks, they're coming out of my ears. – tommytwoeyes Nov 10 '15 at 22:50
  • @JW Ok, thanks! So that's the only criterion that makes a power series geometric? – tommytwoeyes Nov 10 '15 at 22:52
  • 1
    So surely you see the answer now, but I'll state it for the record: a power series is a geometric series if its coefficients are constant (i.e. all the same). In particular, not all power series are geometric. For example $\sum x^n$ is geometric, but $\sum \frac{x^n}{n!}$ is not. – ziggurism Nov 10 '15 at 22:53
  • The criterion for a geometric series is that the ratio of successive terms is the same constant. Also note that relative to the sum, x is constant. – john May 23 '18 at 05:56

1 Answers1

1

A geometric series is characterized by its fixed ratio $r$ and starting term $a$. Therefore, we can represent a geometric series in a number of ways.

$a + ar + ar^{2} + \cdots = \sum\limits_{n = 0}^{\infty} ar^{n}$

A power series is a polynomial characterized by increasing powers of a variable centered at some value $c$ multiplied by coefficients.

$a_0(x - c)^{0} + a_1(x - c)^{1} + a_2(x - c)^{2} + \cdots = \sum\limits_{n = 0}^{\infty}a_n(x - c)^n$.

enter image description here

Look at the relationship between the two mathematical structures. From this, we can conclude that a geometric series is a power series in the specific case that the power series has constant coefficients and $c = 0$. Because a geometric series is a power series, it inherits the usual properties such as radius of convergence.

Neel Sandell
  • 296