If the sample size $n$ is "large" and neither the success probability $p$ nor the failure probability $q=1-p$ is "too small", the binomial distribution is well approximated by the normal distribution with mean $\mu = n p$ and standard deviation $\sigma = \sqrt{n p q}$.
To be more specific: If the three conditions $n\ge 50$, $n p \ge 10$, and $n q \ge 10$ are satisfied, the approx. is great.
This can be checked by plotting the probability density functions, which I did for our example with $n=1000$, and $p=1/2$ in the region of interest:

In order to "resolve" the difference of the two probability densities here an other plot:
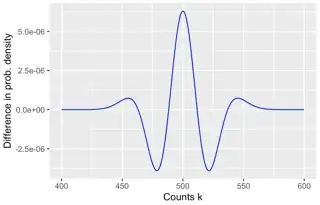
In order to keep it simple, I didn't add any "continuous correction" -- which exists for the approximation. Looking at the plots, we see that the approximation is great. Hence, we are allowed to use the normal approximation to estimate the probability. This was done by the others so I do not repeat it here.