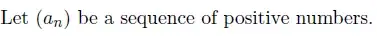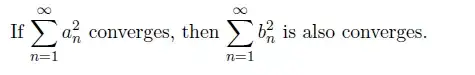If the sequence $b_n$ is defined as $$b_n =\frac {a_1+a_2+\dots+a_n}n.$$
then
I found out that $b_n$ is always divergent and now that I have to prove the given statement I tried using comparison test. The problem is that I am getting that this is true if the sequence $a_n$ in monotonically increasing. But the hypothesis only says that it is a non negative sequence.
This is a special case of Hardy's inequality. Also, you probably meant "monotonically decreasing" instead of "increasing"; (obviously an increasing sequence of positive numbers does not converge to zero, and in particular is not square summable.) If you do have a proof for any decreasing positive sequence $a_n$, then you can easily reduce the general case to that case: let $a_n^{*}$ be the non-increasing rearrangement of $a_n$. Then $b_n^*\geq b_n$ but $\sum_{n=1}^{\infty}a_n^2=\sum_{n=1}^{\infty}(a_n^{*})^2$, so it is sufficient to deal with a non-increasing sequence. You may find this paper interesting, too.
