Let $\psi$ be an analytic function. How do we construct a bounded smooth function $\Phi$ that equals $\psi$ over some domain?

Question

Let $\psi: \mathbb R \to \Bbb R$ be a given analytic function.

How can I construct a smooth (that is, infinitely differentiable) function $\Phi:\Bbb R\to \Bbb R$ such that $\psi|_D=\Phi|_D$ for some interval $D$, and $\Phi$ is bounded above and below?

E: I've been reminded in the comments that such an analytic $\Phi$ isn't possible, I'm changing my request to just infinitely differentiable.

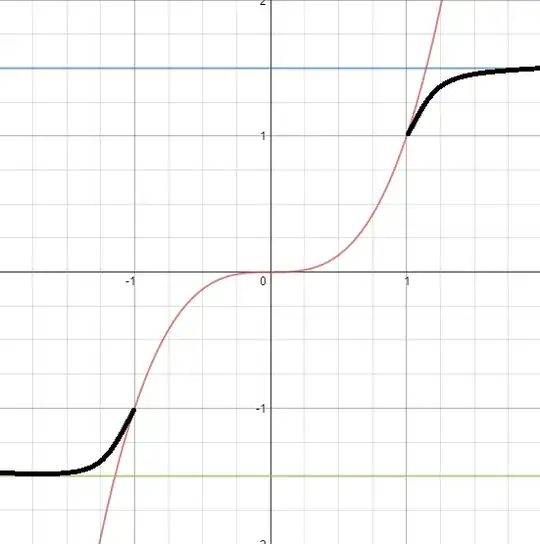
Example:

Red is $\psi(x)=x^3$, blue is $y=1.5$, green is $y=-1.5$. I want to construct a $\Phi(x)$ that looks exactly like $\psi$ for $-1\leq x\leq 1$ and is bounded like the black part of the diagram.

You can't, the new function can almost be smooth, if two analytic functions are the same on an open set, then it has to be the same everywhere. http://math.stackexchange.com/questions/739476/the-identity-theorem-for-real-analytic-functions — , Oct 08 '15 at 23:33
The best you can do is that $\Phi$ is infinitely differentiable. — Plutoro, Oct 08 '15 at 23:45
Oh, that's true, I completely overlooked that fact, I'll change the question a bit then. — YoTengoUnLCD, Oct 08 '15 at 23:57
@AlfredYerger Could you elaborate on how to do that? SangchulLee What do you mean? — YoTengoUnLCD, Oct 09 '15 at 00:12

score 1 · Answer 1 · answered Oct 09 '15 at 00:07

1

Hint: look up "bump function".

answered Oct 09 '15 at 00:07

Robert Israel

470,583

score 0 · Answer 2 · answered Oct 09 '15 at 00:09

0

It still may be impossible.For example if $$f(0)=0,$$ $$f(x)=e^{(-1/x^2)} , x\neq 0$$ then $f$ cannot be extended to an analytic function on any open domain $D\subset C$ for which $0\in D$.

answered Oct 09 '15 at 00:09

DanielWainfleet

59,529

Let $\psi$ be an analytic function. How do we construct a bounded smooth function $\Phi$ that equals $\psi$ over some domain?

2 Answers2