What are the coefficients required to finish a regular pentagon given
that two edges are known?
The answer is $1$ and the Golden ratio $\phi=(1+\sqrt{5})/2$. See the proof below:
These coefficients are two invariant of a pentagon. That is, no
matter its size or orientation the coefficients are the same.
If two edges are adjacent we can, without loss of generality, consider
that they have $O=(0,0,0)$ as their common vertex. Even more,
since the coefficients that we are looking for are invariant, we
can consider the problem in the plane $\mathbb{R}^2$.
The five points of a pentagon are easily found by solving the
equation $x^5 + 1 = 0$. These are given by:
\begin{eqnarray}
x_1 &=& 1 \quad , \quad y_1 = 0 \\
x_2 &=& \cos \theta \quad , \quad y_2 = \sin \theta \\
x_3 &=& \cos 2 \theta \quad , \quad y_3 = \sin 2 \theta \\
x_4 &=& \cos 3 \theta \quad , \quad y_4 = \sin 3 \theta \\
x_5 &=& \cos 4 \theta \quad , \quad y_5 = \sin 4 \theta,
\end{eqnarray}
with $\theta=2 \pi/5=72^{\circ}$.
We want to push these solutions so that one of the vertices is 0.
At the moment the solutions are centered at 0. We can do this
by subtracting the vertex $(x_4,y_4)$ from all other vertices and getting
the coordinates (sorted in counter-clockwise order)
\begin{eqnarray}
A &=& (1-\cos 3 \theta , - \sin 3 \theta) \\
B &=& (\cos \theta - \cos 3 \theta, \sin \theta - \sin 3 \theta) \\
C &=& (\cos 2 \theta - \cos 3 \theta, \sin 2 \theta - \sin 3 \theta) \\
D &=& (0,0) \\
E &=& (\cos 4 \theta - \cos 3 \theta, \sin 4 \theta - \sin 3 \theta)
\end{eqnarray}
The figure below shows the pentagon before (left) and after (right) being pushed up to have the origin $O=(0,0)$ as one its vertices.

The vector equations to get to the vertex $A$ are
\begin{eqnarray}
\alpha E + \beta C &=& A
\end{eqnarray}
This is a simple system of two linear equations with two unkonwns.
The solutions are:
\begin{eqnarray*}
\alpha &=& 2 \cos \theta - 1. \\
\beta &=& 4\,\cos ^2\theta+2\,\cos \theta
\end{eqnarray*}
Since for the pentagon $\theta=2 \pi/3=72^{\circ}$ the numerical evaluation for this is
\begin{eqnarray}
\alpha &\approx& 1.618033988749895 \\
\beta &=& 1.
\end{eqnarray}
It is interesting, due to the symmetry of the problem that
the coefficients to get to $B$ are the same but in reverse order.
That is $\beta, \alpha$.
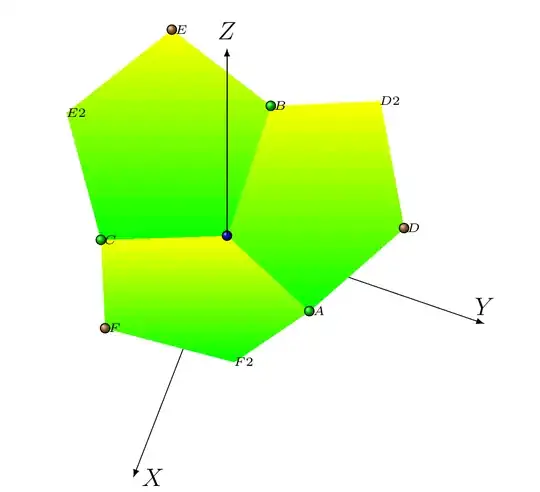
To test this I built the bottom layer of a dodecahedron which consists
of three pentagons. We assume that we know the bottom vertex at $O=(0,0,0)$
(the blue dot at the center) and
three other vertices $A,B,C$ separated (green color) $120^{\circ}$. The result of the
computation of the other 6 vertices (brown color,no ball for indexed 2 vertices) are shown . They are computed
from the following simple formula
\begin{eqnarray}
D= \alpha A + \beta B \\
D2= \beta A + \alpha B \\
E= \alpha B + \beta C \\
E2= \beta B + \alpha C \\
F= \alpha C + \beta A \\
F2= \beta C + \alpha A \\
\end{eqnarray}
where $\alpha=1.618962432915921$ and $\beta=1$.
The figure was computed using
https://en.wikipedia.org/wiki/PGF/TikZ
using the equations above.
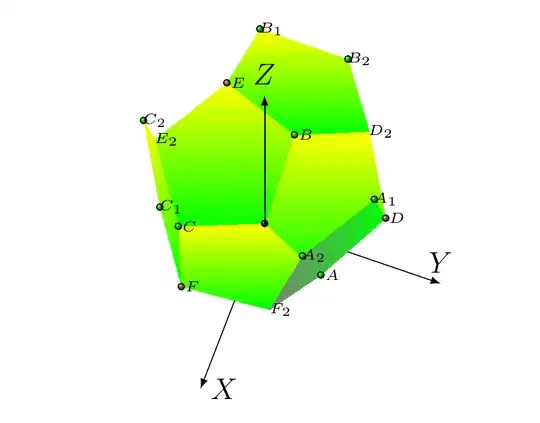
With the new vertices we can construct new ones by using recursively the same idea. For example:
\begin{eqnarray*}
A_1 &=& A + (F_2 -A) + \alpha (D-A) = F_2 + \alpha (D-A) \\ A_2 &=& A + \phi (F_2 -A) + (D-A) = D + \alpha (F_2-A) \\
B_1 &=& B + (D_2 -B) + \alpha (E-B) = D_2 + \alpha (E-B) \\ B_2 &=& B + \phi (D_2 - B) + (E-B) = E + \alpha (D_2-B) \\
C_1 &=& C + (E_2 -C) + \alpha (F-C) = E_2 + \alpha (F-C) \\ C_2 &=& C + \phi (E_2 - C) + (F-C) = F + \alpha (E_2-C) \\
\end{eqnarray*}
Provides 6 new vertices and three new faces. We show the figure for this, which corresponds to half of a dodecahedron. The algorithm shown here becomes a simple algorithm without the need to compute complicated equations. Just adding vectors and scaling some of them with $\alpha$.
It is interesting to see that $\alpha$ is the Golden ratio
http://mathworld.wolfram.com/GoldenRatio.html
This suggest a pure geometrical proof:
In the first figure right frame (in red) figure, the segment that joints $C$ to $A$ is the vector
$A-C$, and it is parallel to the vector $E$. Then we know
that the ratio between a diagonal and the side of a pentagon is
the Golden ratio $\phi$. That is
\begin{equation}
\phi = \frac{|A - C|}{|E|}.
\end{equation}
So the scalar required to get to $A$ through $E$ is exactly the
Golden ratio $\phi$. Then
$A = \phi E + C$, from which the coefficients become
$\alpha=\phi=(1+\sqrt{5})/2 \approx1.61896243291592 $ and $\beta=1$.
For the construction of the whole dodecahedron visit this website:
Cleverest construction of a dodecahedron / icosahedron?


