The $5n+1$ Problem

Question

The Collatz Conjecture is a famous conjecture in mathematics that has lasted for over 70 years. It goes as follows:

Define $f(n)$ to be as a function on the natural numbers by:

$f(n) = n/2$ if $n$ is even and $f(n) = 3n+1$ if $n$ is odd

The conjecture is that for all $n \in \mathbb{N}$, $n$ eventually converges under iteration by $f$ to $1$.

I was wondering if the "5n+1" problem has been solved. This problem is the same as the Collatz problem except that in the above one replaces $3n+1$ with $5n+1$.

Answer 1

You shouldn't expect this to be true. Here is a nonrigorous argument. Let $n_k$ be the sequence of odd numbers you obtain. So (heuristically), with probability $1/2$, we have $n_{k+1} = (5n_k+1)/2$, with probability $1/4$, we have $n_{k+1} = (5 n_k+1)/4$, with probability $1/8$, we have $n_{k+1} = (5 n_k+1)/8$ and so forth. Setting $x_k = \log n_k$, we approximately have $x_{k+1} \approx x_k + \log 5 - \log 2$ with probability $1/2$, $x_{k+1} \approx x_k + \log 5 - 2 \log 2$ with probability $1/4$, $x_{k+1} \approx x_k + \log 5 - 3 \log 2$ with probability $1/8$ and so forth.

So the expected change from $x_{k}$ to $x_{k+1}$ is $$\sum_{j=1}^{\infty} \frac{ \log 5 - j \log 2}{2^j} = \log 5 - 2 \log 2.$$

This is positive! So, heurisitically, I expect this sequence to run off to $\infty$. This is different from the $3n+1$ problem, where $\log 3 - 2 \log 2 <0$, and so you heurisitically expect the sequence to decrease over time.

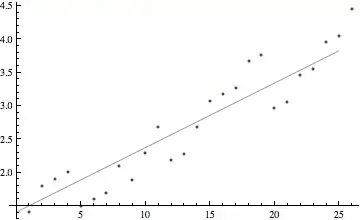
Here is a numerical example. I started with $n=25$ and generated $25$ odd numbers. Here is a plot of $(k, \log n_k)$, versus the linear growth predicted by my heuristic. Notice that we are up to 4 digit numbers and show no signs of dropping down.

Answer 2

In Part I of Lagarias' extensive, annotated bibliography of the $3x+1$ problem, he notes a $1999$ paper by Metzger (reference $112$) regarding the $5x+1$ problem:

For the $5x + 1$ problem he shows that on the positive integers there is no cycle of size $1$, a unique cycle of size $2$, having smallest element $n = 1$, and exactly two cycles of size $3$, having smallest elements $n = 13$ and $n = 17$, respectively.

It is unclear from the notes whether the paper shows that these are the only cycles of the $5x+1$ problem or whether there may exist longer cycles.

Answer 3

Using a Python program, I calculated the orbit starting at 7. It seems to diverge to infinity with exponential speed. I calculated till the numbers exceeded $10^{1000}$. So probably, not every number will end up at 1. And not all numbers will end up in a cycle.

Initially, my program returned to 7 after a large number of steps. However, it turned out that the program made small errors when the numbers became very large. Using the decimal module resolved this problem.

Here is the code that I used:

from decimal import *
getcontext().prec=1001
def collatz5(n):
    if n%2 == 0:
        return Decimal(n)/Decimal(2)
    else:
        return Decimal(5)*Decimal(n)+Decimal(1)
n=7
for i in range(100000):
    if n>10**1000:
        print("bound exceeded")
        print("number of steps: ",i)
        break
    n=collatz5(n)