Is this function $f(x)=x^{-1/3}$ continuous, when $x$ varies from $-1$ to $1?$

Question

I have doubt ! regarding to this question ,

Is this function $f(x)=x^{-1/3}$ continuous, when $x$ varies from $-1$ to $1?$

As I read, when left limit is not equivalent to right limit ,then function is not continuous . For this function $f(x)=x^{-1/3}$ should not be continuous , since it's undefined at $x=0$ , check-here or here

score 5 · Accepted Answer · answered Sep 28 '15 at 09:22

5

In modern mathematics, the definition of continuity discards points that fall outside the domain of definition. In other words, continuity must be checked only at point of the domain. Since your function is defined on $\mathbb{R} \setminus \{0\}$, it is continuous at every point of its domain of definition.

answered Sep 28 '15 at 09:22

Siminore

35,786

Well , in linked-question , are all statements true ? – hululu Sep 28 '15 at 09:30
In my opinion, the first question is almost meaningless. As I said, it is rather unfair to ask whether a function is ocntinuous outside its domain. – Siminore Sep 28 '15 at 09:38
You are correct sir , but $f$ belongs in $[-1,1]$ – hululu Sep 28 '15 at 09:57
No, $[-1,1]$ is not a subset of the domain of $f$. Unless, of course, you decide to define $f(0)=$ something. In this case, the extended function will be discontinuous. – Siminore Sep 28 '15 at 10:04
so , I cancluded $f$ is continous everywhere except $x=0$ , rt ? – hululu Sep 28 '15 at 11:32
sir , I want more discussion http://math.stackexchange.com/questions/1495246/if-a-function-is-not-continuous-then-is-it-possible-for-bounded-function-in-give – hululu Oct 24 '15 at 13:54

score 1 · Answer 2 · answered Sep 28 '15 at 09:33

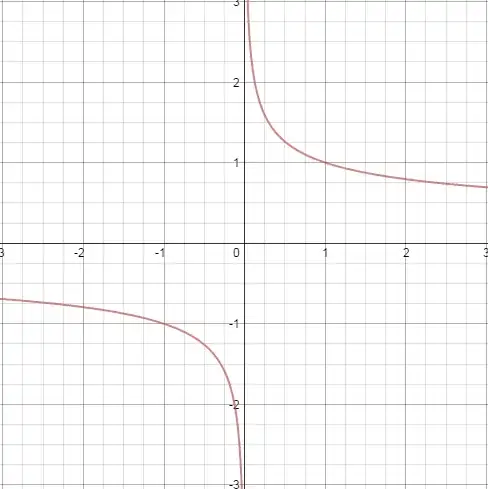
You're right: It only makes sense to say that a function $f$ is continuous in $x$ if $x$ is in the domain of $f$, i.e. if $f$ is defined in $x$.

Let me add that for other examples it could be possible that $f$ can be extended to a continuous function $$ \tilde{f}(x) = \begin{cases} f(x), &x\neq 0,\\ c, & x=0,\end{cases} $$ with some value $c\in\mathbb{R}$, which is then a function defined on the larger domain $[-1,1]$ including $x=0$ (one says that $f$ possesses a removable discontinuity in $0$ if that works). You only obtain a continuous function by that process if $c = \lim_{x\nearrow 0} f(x) = \lim_{x\searrow 0} f(x)$ and this is obviously not the case in your example, since $\lim_{x\nearrow 0} f(x) = -\infty \neq \infty = \lim_{x\searrow 0} f(x)$.

Is this function $f(x)=x^{-1/3}$ continuous, when $x$ varies from $-1$ to $1?$

2 Answers2

Linked