When we have the power set $2^S$, does the 2 actually mean anything?

Question

I have seen that most math books refer to the power set as $2^S$, usually in a cursory manner and without much detail. I was wondering if the 2 meant anything, because I normally just interpret it as a cardinality thing, like if S has two elements, then the power set has $2^2 = 4$ elements. Thanks!

Answer 1

In fact, if $A$ and $B$ are sets, then it is common to define $$ A^B = \{f \mid f \text{ is a function from $B$ to $A$}\} $$ You may want to prove that $|A^B| = |A|^{|B|}$ holds for finite sets, as the notation suggests. With this notation, one may take $2 = \{0,1\}$ (or any set of 2 elements) so that $2^S$ is the set of functions from $S$ to $\{0,1\}$. We can associate any $f \in \{0,1\}^S$ with the subset $$ S_f = \{s \in S: f(s) = 1\} $$ This association is bijective, so our version of $2^S$ can be naturally thought of as the power set of $S$.

Answer 2

If $A$ and $B$ are two sets, the notation $A^B$ is used to the set of all functions from $B$ to $A$. Now $\mathcal{P}(S)$ can be identified with the set of all functions from $S$ to $\{0, 1\}$ if we identify every subset of $S$ with the corresponding indicator function. This way we get a bijection $\mathcal{P}(s) \leftrightarrow \{0, 1\}^S$.

It isn't important that the set $\{0, 1\}$ consists exactly of the two elements $0$ and $1$, it is important that it contains exactly two different values. The shortened notation $2^S$ is derived from this observation.

Answer 3

Here’s a (hopefully) intuitive way to think about it. This is a longwinded version of Ben’s answer.

tl;dr: enumerating all subsets of $X$ is like enumerating all functions from $X$ to $\{0, 1\}$. $\{0, 1\}$ contains two elements, so the power set is $\{0, 1\}^X$, or $2^X$.

But where is $\{0, 1\}$ coming from?..

---

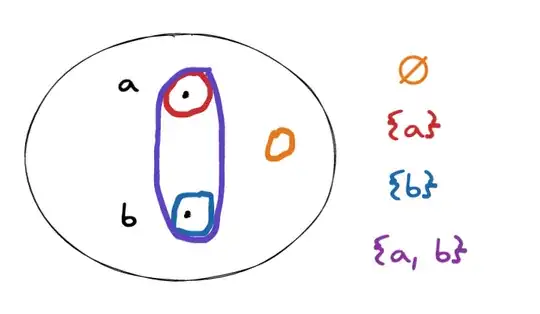
Suppose you have a set of $X = \{a, b\}$.

Its power set is a set of all its subsets. If you were to write it down, you would end up with $\mathcal{P}(X) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\}$. But how did you arrive at this? For each subset, you’d open the curly braces, decide for each element whether you want to include it this time or not, and repeat until you’ve found all combinations. Visually, you could represent this process like this:

However, you can also think of this process as a sort of a mapping.

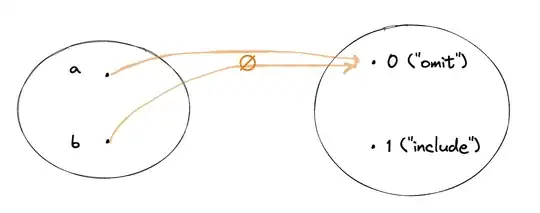
Whenever you construct a subset, you make a bunch of decisions. For each element, you decide whether to include it or not. Let’s draw a decision as an arrow that goes from each original element in $X$ either to $0$ (“omit”) or to $1$ (“include”).

For example, an empty set (subset of $X$) omits both elements:

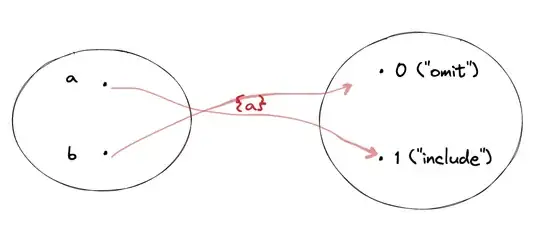
The $\{a\}$ subset of $X$ includes $a$ but omits $b$:

The $\{b\}$ subset of $X$ includes $b$ but omits $a$:

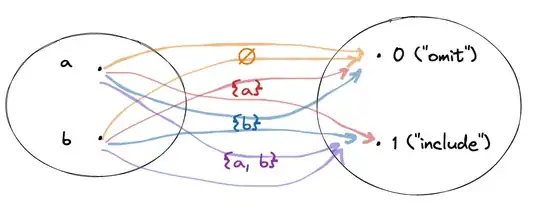
So each subset of $X$ can be represented as a bunch of arrows from elements of $X$ to a “decision” between $\{0, 1\}$. But this is also how you can represent a function. A function, loosely speaking, is a bunch of arrows from the input to the output. So, you could think of these colored arrows in two ways:

1. You could think of each color as a distinct subset of $X$.
2. Or you could think of each color as a function from $X$ to $\{0, 1\}$.

It turns out that we’ve done something interesting here. We were trying to enumerate all subsets of $X$. While doing so, we have enumerated all possible functions from $X$ to $\{0, 1\}$.

Now here’s the key part. We know separately that if you try to enumerate all possible functions from $A$ to $B$, you end up with a set denoted as $B^A$. As you might guess, its size is $|B|^{|A|}$.

Our set on the left is $X$, and our set on the right is $\{0, 1\}$. Thus, the set of all functions from $X$ to $\{0, 1\}$ is $\{0, 1\}^{X}$. The exact $0$ and $1$ values don’t matter (it only matters that we have two of them — “omit” and “include”), so we'll write it as $2^{X}$. And indeed, its number of elements is $2^{|X|}$.

To sum up, enumerating all subsets of $X$ is like enumerating all functions from $X$ to $\{0, 1\}$. $\{0, 1\}$ contains two elements ($0$ is “omit”, $1$ is “include”), so the power set is $\{0, 1\}^X$, or $2^X$.

---

Finally, here is an intuitive way to see where exactly the $2$ comes up in practice.

Suppose we add $c$ to our original set $\{a, b\}$. How much will the power set grow? We’re gonna need two versions of all the subsets we had previously: one version where $c$ is included, and one version where $c$ is omitted. So adding $c$ alone to the original set has doubled the power set. Adding $d$ to the original set will double the power set again. Again, this happens before there are two things that can happen with each new element: either it’s omitted, or it’s included. Hence, $2^{|X|}$ subsets.

Answer 4

Yes, the notation for power set of set $X$ is mostly denoted by $2^X$, by $\mathrm{Pow}(X)$ or $\mathcal{P}(X)$. The first notation is related to cardinality, because for finite sets, $|\mathrm{Pow}(X)| = 2^{|X|}$, so the notation $2^X$.

Answer 5

The power set is the set of all subsets of $S$, these subsets have cardinality ranging from $0$ (the empty set) to $n$ (the whole set $S$ ). If $n$ is the cardinality of $S$ then the number of subsets of cardinality $k$ is $\displaystyle{n\choose k}$ and the number $2$ is justified by the following formula that gives the number of all subsets of $S$ :

$$\sum_{k=0}^{n}{n\choose k}=2^n$$

Answer 6

The $2$ is present because there are $S$ binary decisions that have to be made. So there are $2^S$ ways to form a subset.