Yes, this is possible. Define $f$ as follows. For $x\leq 0$, $f(x)=-x$. If $n\in\mathbb{N}$, then
$$f(n+x)=\begin{cases} n+3x &\text{ if }0\leq x\leq 1/3 \\ n+2-3x &\text{ if }1/3\leq x\leq 2/3 \\ n-2+3x &\text{ if }2/3\leq x\leq 1 \end{cases}$$
A glance at a graph shows that $f$ is continuous and achieves every positive value four times, achieves the value $0$ twice, and is never negative.
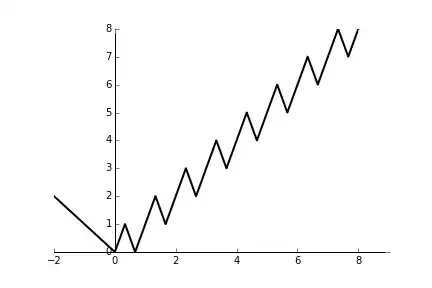
On the other hand, it is impossible for every point in the range of $f$ to have the same even number of preimages. For a contradiction, suppose $n$ is an even integer and $f:\mathbb{R}\to\mathbb{R}$ achieves every value in its range exactly $n$ times. Fix some value $a\in f(\mathbb{R})$ and let $x_1<x_2<\dots<x_n$ be the preimages of $a$. Let $p$ be the number of $x_i$ which are local minima of $f$, $r$ be the number of $x_i$ which are local maxima of $f$, and $q$ be the number of $x_i$ which are neither. Then it follows from the intermediate value theorem that if $\epsilon>0$ is sufficiently small, $f$ achieves the value $a+\epsilon$ at least $2p+q$ times near the $x_i$ and $f$ achieves the value $a-\epsilon$ at least $2r+q$ times near the $x_i$. Thus $2p+q\leq n$ and $q+2r\leq n$. But $p+q+r=n$, and so adding these two inequalities together we find that actually $2p+q=n=2r+q$ and thus $p=r$. Since $n$ is even, this implies $q=n-p-r$ is also even.
That is, there are an even number of $x_i$ at which $f(x)-a$ changes sign. Thus $f(x)-a$ has the same sign on both components of $\mathbb{R}\setminus [x_1,x_n]$. Suppose WLOG that $f(x)-a$ is always positive on $\mathbb{R}\setminus [x_1,x_n]$. It follows that $f$ has a global minimum value $b$ which it achieves somewhere on $[x_1,x_n]$.
But now replace $a$ by $b$ and repeat the argument above. Every preimage of $b$ must be a local minimum, so $p=n$, which is clearly impossible. This contradiction means that no such $f$ can exist.
