Can anyone suggest an example of non-homeomorphic spaces $X$ and $Y$ such that $X \times X$ and $Y \times Y$ are homeomorphic?
Asked
Active
Viewed 375 times
7
-
2http://mathoverflow.net/questions/66007/can-non-homeomorphic-spaces-have-homeomorphic-squares – sdcvvc Sep 12 '15 at 12:01
-
I don't think you will get easy examples of that – Sep 12 '15 at 12:06
-
An example is the whitehead manifold. If $X$ is the whitehead manifold, then $X \times X \cong \Bbb R^6$ even though $X$ is not homeomorphic to $\Bbb R^3$. – Balarka Sen Sep 12 '15 at 12:34
1 Answers
10
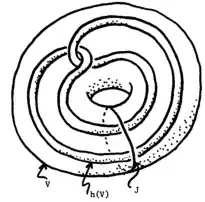
Start with a collection of solid torii $\{T_i\}$ with each $T_{n+1}$ embedded in $T_n$ as follows
Then the complement of the nested intersection, namely, $\Bbb S^3 \setminus \bigcap T_i$ is called the Whitehead manifold, which we will denote by $W$. $W$ is not homeomorphic to $\Bbb R^3$ as it is not simply connected at infinity (which is surprising, as $W$ is contractible since each $\Bbb S^3\setminus T_n$ is nullhomotopic in $\Bbb S^3 \setminus T_{n+1}$)
In Glimm, Two cartesian products which are euclidean spaces, Bull. Soc. Math. France $88 (1961), 131-135$, available here, it is proved that $W \times W \cong \Bbb R^6 \cong \Bbb R^3 \times \Bbb R^3$.
Thus, $X = W$ and $Y = \Bbb R^3$ provides an example of such a space.
Balarka Sen
- 14,380
-
I think your first line has a typo... $T_{n+1}$ is embedded in $T_n$ ... – Anubhav Mukherjee Sep 12 '15 at 14:45
-