0

It is quite possible to show mutually exclusive events using Venn Diagram; two sets having no intersection that is they are disjoint.

disjoint sets

But what about independent events? How is Venn Diagram used then? $P(A\cap B)= P(A)\cdot P(B)$. There must be intersection or overlapping of the two events $A$ & $B$.

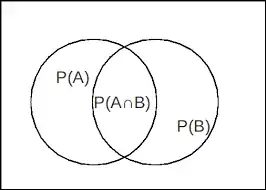
dependent sets

But, then how can diagram be different from two dependent sets?

Now, if one sees the the diagram & is asked to find the probability of occurance of $A$ given $B$ has occured, he will definitely do this by $$P(A|B)= \frac{P(A\cap B)}{P(B)}$$ But $A$ & $B$ are independent events. This Venn diagram does not reflect it at all. I'm really confused how to draw a Venn diagram for independent events.

I am having a hard time in distinguishing between the difference between intersection of dependent events & intersection of independent events. Can anyone help me distinguish them?

Ben Steffan
  • 8,325
  • Are you claiming that every pair of dependent events has a Venn diagram like your second diagram with a non-empty intersection? If so, why do you say that? – David K Sep 08 '15 at 02:45
  • @David K: Except mutually exclusive events, right? –  Sep 08 '15 at 03:33
  • There are various ways events can be dependent. I can think of several different Venn diagrams that could correspond to dependent events. – David K Sep 08 '15 at 04:43
  • @David K: Could you please, elaborate? –  Sep 08 '15 at 07:28
  • In any example where $P(A\cap B) \neq P(A)P(B)$, the events $A$ and $B$ are dependent. So the events could be disjoint, or we could have $A\subsetneq B$, $B\subsetneq A$, or even $A=B$; or it could as in your second diagram, but with a larger or smaller intersection than independent events would have. So basically, draw any Venn diagram for two sets $A$ and $B$ that are non-empty and are each less than the entire probability space, and you can find an example of dependent events like that. – David K Sep 08 '15 at 12:00
  • Possible duplicate of Can one infer independence by simple reasoning/intuition? – BCLC May 26 '18 at 17:11

1 Answers1

1

If and only when the events are independent, then we have: $\mathsf P(A)=\dfrac{\mathsf P(A\cap B)}{\mathsf P(B)}$

This fact isn’t illustrated on the Venn diagram, unless the probability measure of the shapes in the diagram are proportional to their area, in which case independence means:

$$\dfrac{\lVert A\rVert}{\lVert \mathcal U\rVert}=\dfrac{\lVert A\cap B\rVert}{\lVert B\rVert}$$

Graham Kemp
  • 133,231
  • Thanks, sir,for the answer ._ unless_ the probability measure of the shapes in the diagram are proportional to their area- can you please explain it; I couldn't conceive it. –  Sep 07 '15 at 16:46
  • Sometimes, it is not even possible to visualise the intersection in the diagram. For example, let there be an urn containing marked balls. Let the events $A$ & $B$ denote the events of drawing evenly-marked ball at the first draw & odd-one at the second draw respectively without any replacement. Thus $A$ & $B$ are independent events. So, $P(A\cap B)= P(A)\cdot P(B)$. But can you visualise the intersection between $A$ & $B$? $A$ contains elements $2,4,6,\ldots$ while $B$ has elements $1,3,5,\ldots$. How could then there be overlap between $A$ & $B$?? Can you explain this, please? –  Sep 07 '15 at 16:54
  • 1
    If you want to describe $P(A\cap B)$, you must create a probability space that accounts for both balls that are drawn. It is not enough for $A$ to be just the set ${2,4,6,\ldots}$ and for $B$ to be ${1,3,5,\ldots}$, because then $A$ and $B$ would be disjoint (no elements in common), so $P(A\cap B)$ would be $0$, and you know that's not true. A better probability space has elements like $(1,2)$, $(2,1)$, $(1,3)$, $(3,1)$, $(2,3)$, $(3,2)$, etc. If you do this correctly you will find that $A$ and $B$ are not independent events. – David K Sep 08 '15 at 12:12
  • @user36790 It just means $\lVert A\rVert\propto \mathsf P(A)$, that is where you draw the size of the shapes representing the events (and their overlap) to be proportional to their probability. – Graham Kemp Sep 08 '15 at 13:03