Why are natural numbers countable?

Question

I get how Cantor's diagonalization argument works for real numbers, but I don't see why you can't apply the same logic to natural numbers. I was reading this thread, but the explanations weren't intuitive to me, never taken set theory.

Answer 1

Definition - A set $S$ is countable iff there exists an injective function $f$ from $S$ to the natural numbers $\mathbb{N}$.

Cantor's diagonal argument - Briefly, the Cantor's diagonal argument reads as follow:

Take $S = (0, 1) \subset \mathbb{R}$ and suppose that there exists an injective function $f$ from $S$ to $\mathbb{N}$. Then, we prove that there exists an $s \in S$ (the diagonal number) such that $f(s)$ is not defined (i.e. there is no $n \in \mathbb{N}$ such that $f(s) = n$). Hence, $f$ is not an injective function and $S$ is not countable, or alternatively uncountable.

Is $\mathbb{N}$ countable? - If you are concerned to prove this, just consider the function $$f(n) = n.$$ Obviolusly, this is a injective function since for every $n \in S = \mathbb{N}$, there is an $f(n)$ in $\mathbb{N}$. So, $\mathbb{N}$ is countable.

Is the set of even number countable? - Let $S$ be the even numbers set. Consider $$f(s) = \frac{s}{2}.$$ Again, this is a injective function, since for every even number $s \in S $, there is an $f(s) = \frac{s}{2}$ in $\mathbb{N}$. So, S is countable.

Conclusion - The Cantor's diagonal argument is just a method to prove that there is no injective function between two set. It's a tool to prove something, but it is not the only method for proving countability.

Answer 2

Cantor's diagonal argument applied to any list of natural numbers written in decimal does indeed produce a decimal numeral not on the list.

A decimal numeral gives a natural number if and only if it repeats zeroes on the left; e.g. the number one is $\ldots 00001$.

So, the question you have to ask yourself is: why should the diagonal argument give a decimal numeral that repeats zeroes?

Answer 3

Cantor's diagonalization argument proves that the set $]0,1[$ is uncountable by negating the definition of countable set, i.e.

A set $S$ is called countable if there exists an injective function $f$ from $S$ to $\mathbb N$ (Wikipedia)

Specifically, it tries to describe a bijection from $]0,1[$ to $\mathbb N$ (note that this is the other way around, so he should be constructing at least a surjection) and then proves that it must be an injection by collecting and modifying all digits along a diagonal.

My point is, you don't have to test if $\mathbb N$ is countable because the definition of countability relies on $\mathbb N$! Trivially one can take the identity function in $\mathbb N$ and see that it is indeed an injective function like the one we're looking for.

Answer 4

The myriad other answers to this question more than cover the technical details, so I will try here to give an intuitive answer. The reason why diagonalisation doesn't work on the natural numbers is basically: because they can all be represented using a finite number of digits. OK, you might say, but how does this make them un-diagonalisable? Well, let's try the diagonal argument.

Suppose we have our list of natural numbers $a_1, a_2, a_3, \dots$ and we apply the diagonal construction to construct a number $b$ from an infinite list of digits $b = b_1 b_2 b_3 \dots$ such that digit $i$ of $a_i$ differs from $b_i$, which is digit $i$ of $b$. OK, then clearly this number is outside the set: this is the crux of the diagonal argument.

But is the number $b$ a natural number? Well, for starters, it doesn't look to hopeful, because there are an infinite list of digits $b_i$. Yes, you might say, but what if this infinite list of $b_i$ ends in all $0$s? Then we can just ignore the $0$s and interpret the rest as a natural number. But can $b$ end in an infinite string of $0$s?

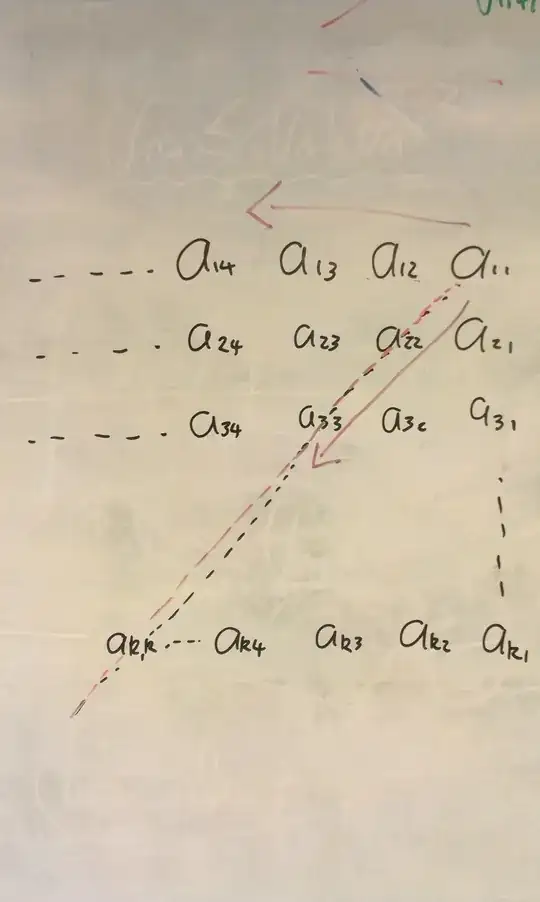
The answer is no. Here's why. For the contradiction to work, we must have first assumed that all the natural numbers were in our list. From this, we can show that for every sufficiently large $i$, there is some $j$ such that $a_{j, j} = 0$ and so $b_j \neq 0$. Here $a_{j, k}$ just means digit $k$ from the number $a_j$ (as per diagram below). To prove this result, we consider the set of all numbers $A_i = \{a_1, a_2, \dots, a_i\}$. Now, either this is equal to the set $S_i = \{1, 2, \dots, i\}$, or there is some element of the set $S_i$ that is not in $A_i$. In either case, there is clearly a number not already in the list of at most $\log ({i + 1}) + 1$ digits i.e. its most significant digit is at most at position $\log ({i + 1}) + 1$. Since the log function grows much slower than linear, we know for sufficiently large $i$, $\log ({i + 1}) + 1 < i$. And so for all $j > i$, $\log ({i + 1}) + 1 < j$. Now, the number must appear somewhere, so it is equal to some $a_j$. But by $\log ({i + 1}) + 1 < j$, then $a_{j, j} = 0$, and so $b_j \neq 0$. Since we assumed an arbitrary $i$, this happens infinitely often, so $b$ has infinitely many non-zero entries. Thus $b$ can't be a natural number.

OK, maybe that strayed a bit from intuition... but basically, the idea is that the diagonal construction doesn't guarantee you a natural number, it only guarantees you a real number- because all infinite digit representations are real numbers, but not all are natural numbers.

Below: image for constructing a diagonal from the list. Note we go from top right to bottom left, starting as the least significant digit and moving to the most significant. Also, the least significant digit is at the far right of each number i.e. $a_{k, 1}$, as is the usual convention.