distribution of one random over the sum of random variables

Question

Suppose that $X_1,\ldots,X_n$ are independent random variables with $X_i\sim Gamma(\alpha_i,\beta)$. Define $U_i=\frac{X_i}{X_1+\cdots+X_n}$ for $i=1,2,\ldots,n$. Show that $U_i\sim Beta(\alpha_i,\sum_{j\neq i}\alpha_j)$. This is a question of past comprehensive exam. It also gave a hint: Think of $U_i$ as $X_i/(X_i+W)$, where $W=\sum_{j\neq i}X_j$ is independent of $X_i$. Can someone give me more hint about it?

https://math.stackexchange.com/a/190695/321264 – StubbornAtom Mar 26 '20 at 14:51 — StubbornAtom, Mar 26 '20 at 14:51

score 3 · Answer 1 · answered Sep 04 '15 at 03:30

Result: $$X\sim Gamma(\alpha_1,\lambda) \hspace{5pt} \text{indep of}\hspace{5pt} Y\sim Gamma(\alpha_2,\lambda)\hspace{5pt} \Rightarrow X+Y \sim Gamma(\alpha_1+\alpha_2,\lambda)\hspace{5pt} \text{indep of}\hspace{5pt} \frac{X}{X+Y} \sim Beta(\alpha_1,\alpha_2)$$

Proof: Let $U=X+Y$ and $V=\frac{X}{X+Y}$ write down the joint density of $(X,Y)$ Calculate Jacobian get density of $(U,V)$. In these procedure you get something stronger namely $X+Y$ and $\frac{X}{X+Y}$ are indep. (of course if $X$ and $Y$ are indep.)

score 1 · Accepted Answer · edited Apr 13 '17 at 12:19

1

Hint: Derive the conditional distribution $P(X_i|W)$ and then use the fact that a sum of gammas is also gamma for the unconditional part $P(W)$. Then you get:

$$P(X_i,W)=P(W)P(X_i|W)$$

edited Apr 13 '17 at 12:19

Community

1

answered Sep 04 '15 at 02:30

Are you implying first get the joint density of $(X_i,W)$, and then, let $U_i=X_i/(X_i+W)$, and $V=X_i+W$. Then,using the transformation to get the joint density of $U_i$ and $V$. And then use marginal to get the distribution of $U_i$? – 81235 Sep 04 '15 at 13:28
@user81235 yep. – Sep 04 '15 at 13:36

score 0 · Answer 3 · answered Sep 04 '15 at 05:42

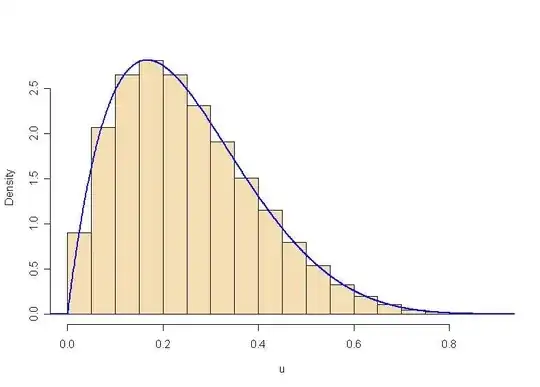
Illustration: The special case $n = 4, \alpha_i = 2,$ for $i = 1, \dots, 4,$ using R to simulatie 100,000 values of $U \sim Beta(2, 6).$

 m = 10^5;  n = 4;  alp = 2
 x = rgamma(n*m, alp, 1)
 DTA = matrix(x, nrow=m, byrow=T)  # each row a sample of 4
 s = rowSums(DTA);  u = DTA[,1]/s  # numerator is first column
 mean(u);  var(u)
 ## 0.2506025    ## approximates E(U)
 ## 0.02084331   ## approximates V(U)

 hist(u, prob=T, col="wheat", main="")
 curve(dbeta(x, alp, (n-1)*alp), n = 1001, lwd=2, col="blue", add=T)

distribution of one random over the sum of random variables

3 Answers3