Intuition for Burnside's Lemma (aka Cauchy-Frobenius Lemma)

Question

Here is the theorem:

Lemma: Let a group $G$ act on a set $S$. Define $\text{Fix}(g)$ as the set of all elements in $S$ fixed by $g$ under this group action. Then the number of distinct orbits of this action, $N$, is $$N=\frac{1}{|G|}\sum_{g\in G}|\text{Fix}(g)|$$

I just took my first semester of abstract algebra and this was really the only theorem for which I couldn't think of some intuitive explanation. The proofs available are not difficult to follow, but for me the result is one of those things that magically appears and you can't see why.

Here is my best effort: the number of orbits in the action is the average number of elements fixed by each permutation, which makes some sense since fixed elements are sort of 'more likely' to be in their own orbit. Thus, when you average out all the fixed elements, you just get the number of orbits.

Of course that doesn't really make sense. I just can't reconcile this arithmetic mean in the midst of a bunch of abstract algebra.

Any thoughts appreciated.

Answer 1

This question was asked here some time ago. I answered it yesterday and a kind user told to not link notes, so I take a chance to put some math here.

As you can see the formula involves the cardinalities of sets, so it is quite natural to ask if you can bring $G$ to the other side and find an explicit isomorphism.

Let's agree on some notation:

• $X$ is a $G$-set, it means that is a set with an implicit action of $G$ on it.

• $O_x$ is the orbit of $x \in X$.

• $G(x, y) = \{g \in G\, .\, y = g x\}$ is the "path space" between $x$ and $y$, so you think to them as "connections" between the two elements.

• $G(x) := G(x, x)$ is then the stabilizer of $x$.

• $X^g = \{x \in X\, .\, g x = x\}$ is the set of elements of $X$ fixed by $g$.

• $X_G$ is the set of orbits, so it is the quotient of $X$ by the equivalence relation induced by the action.

What we want to prove now is that $\displaystyle X_G \times G \cong \sum_{g \in G} X^g$.

As you can find in most algebra textbooks(as Rotman) there is a relation between the fixed points and the stabilizers:

$\displaystyle \sum_{g \in G} X^g = \{(g, x)\, .\, g x = x\} = \sum_{x \in X} G(x)$

So our problem is equivalent to $\displaystyle X_G \times G \cong \sum_{x \in X} G(x)$, but this is just a "global" version of the orbit stabilizer theorem!

Here is a list of (almost) straightforward things I leave you to prove(I have no time right now, if some of them are not clear just ask, or search in the link I put on the other question):

1. If $y \in O_x$ then $G(x, x) \cong G(x, y)$.

2. $G(x, y) \cong G(y, x)$.

3. If $x_1 \sim x_2$ and $y_1 \sim y_2$ then $G(x_1, y_1) \cong G(x_2, y_2)$, in particular if $x \sim y$ then $G(x) \cong G(y)$.

4. Using all that and a bit of tricks on the sums, prove the orbit-stabilizer theorem: $O_x \times G(x) \cong G$.

5. Using all that and a bit of tricks on the sums, prove the global orbit-stabilizer theorem: $\displaystyle \sum_{x \in X} G(x) \cong X_G \times G$.

Addendum:

So, what you can do is to consider $X$ and for each point put an arrow from the point to himself for each element of his stabilizer. Here is an example of what can happen with a group of order $6$ acting on a set of order $11$:

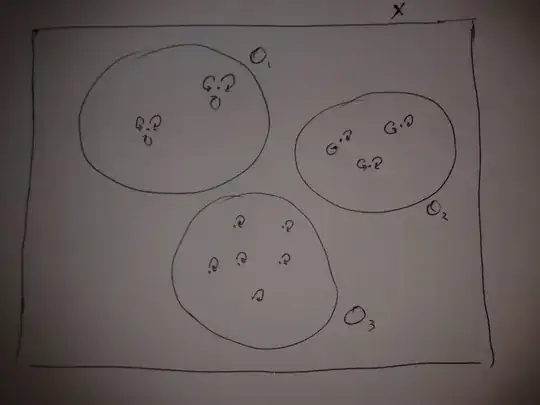
The elements of $X$ are grouped in their classes of equivalence. By (3.) you have a bijection between the sets of arrows of points in the same orbit, and using the orbit-stabilizer theorem you have a bijection between the arrows in one orbit and $G$, so in total you have a bijection between all the arrows of points in $X$ and the product of the orbit space and $G$.