I'm trying to find formulas for hyperbolic functions, starting with this image
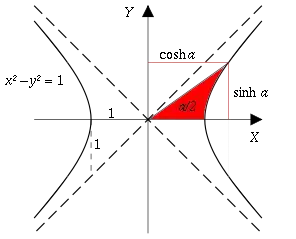
Knowing that the area between the origin, vertex and a point on hyperbola (enclosed by x-axis and hyperbola itself) is equal to $\frac{\alpha}{2}$, I wrote $$ x^2 - y^2 = 1 $$ $$ x = \sqrt{1 + y^2} $$ ... and started integrating this expression for $x$.
$$ \begin{align} \frac{\alpha}{2} & = \int^{y}_0{\sqrt{1 + y^2}\,\textrm{d}y} \\ & = \int^{\arctan y}_0{\sqrt{1 + \tan^2\theta}\sec^2\theta\,\textrm{d}\theta} && \text{let }y = \tan\theta \text{ and }\textrm{d}y = \sec^2\theta\,\textrm{d}\theta \\ & = \int^{\arctan y}_0{\sec\theta\sec^2\theta\,\textrm{d}\theta} \end{align} $$ Here I used integration by parts to find $\int{sec^3\theta\,\textrm{d}\theta}$ $$ \begin{align} \int{\sec^3\theta\,\textrm{d}\theta} & = \sec\theta\tan\theta - \int{\sec\theta\tan^2\theta \,\textrm{d}\theta} \\ & = \sec\theta\tan\theta - \int{\sec\theta(\sec^2\theta - 1) \,\textrm{d}\theta} \\ & = \sec\theta\tan\theta - \int{\sec^3\theta \,\textrm{d}\theta} + \int{\sec\theta \,\textrm{d}\theta} \\ & = \frac{1}{2}\bigg(\sec\theta\tan\theta + \int{\sec\theta \,\textrm{d}\theta}\bigg) \\ & = \frac{1}{2}\bigg(\sec\theta\tan\theta + \ln{\bigg|\sec\theta + \tan\theta \,\bigg|}\bigg) \end{align} $$
... and by substituting $\tan\theta = y$, $\sec\theta = \sqrt{1 + y^2}$ back I got $$ \alpha = y\sqrt{1 + y^2} + \ln{\bigg|\sqrt{1 + y^2} + y \,\bigg|} $$
Which doesn't make much sense, because this is not what an inverse hyperbolic sine looks like. Where have I made mistake? What should I do different?
Thanks.