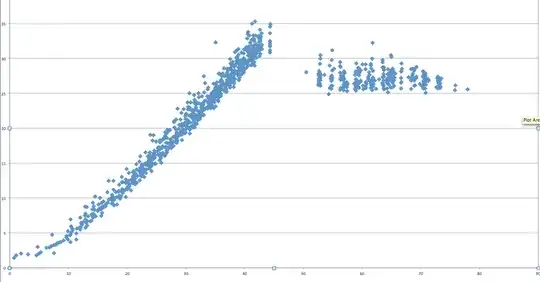
Are there any conjectures from which we can infer something about the first occurrences of prime gaps length $n$ and their distribution? I've made an interesting graph of these values to make this problem easier, with gauss's approximate of their size, $\log(p)$ on the $x$-axis and on the $y$-axis the proportional error, i.e. $\frac{g(p)}{\log(p)}$. A prime gap $g(p)$ is $p_{n+1} − p_n$. What on earth is going on with gaps with error from 25 to 30, why are some of these gaps starting so late, does this pattern continue somehow? I needn't say anything about the nature of the large 'line' but does anyone see the vertical 'wave' like pattern with the anomalistic bunch?
I hope this question doesn't come across as too wordy or vague but would really appreciate any general comment.