Deriving Universal Modus Tollens

Question

I'm asked to derive the validity of Universal Modus Tollens from the validity of Universal Instantiation and Modus Tollens. I'm new to this deriving/proving stuff, so I'm not sure if I'm doing it right, but here's what I came up with:

Universal instantiation says that if (1) is true:

(1) ∀x, P(x) → Q(x)

Then (2) is true for any particular item y

(2) P(y) → Q(y)

Modus Tollens says that if (2) is true and (3) is true:

(3) ~Q(y)

Then (4) is true:

(4) ~P(y)

Therefore if (1) is true, and (3) is true, then (4) is true. In other words, the following argument is valid:

∀x, P(x) → Q(x)
~Q(y)
∴ ~P(y)

And that's Universal Modus Tollens.

Am I doing this right? Am I making any unwarranted assumptions or unsupported claims? Am I skipping any steps?

ThisIsNotAnId · Accepted Answer · 2012-04-29T17:36:40.920

Let's do a little logic magic, shall we?

Note: I will assume here "$\implies$" is identical with "$\rightarrow$", and therefore that you are asserting the proposition in (1) rather than merely considering it. See discussion here for a reason why.

Let the set $S$ be the set of those elements, $x$, such that statements such as "$P(x)$" or "$Q(x)$" make sense and for such statements it makes sense to consider the propositions of the form "$P(x) \implies Q(x)$".

Consider then, since:

$$ \tag{1} \forall x \in S,P(x) \implies Q(x), $$

$$ (1) \iff \tag{2} \forall x \in S, (\text{~}P(x) \vee Q(x)) \text{ is true.} $$

Asserting:

$$ \tag{3} \exists y \in S, \text{~}Q(x) \text{ is true}, $$

we get,

$$ \tag{4} (\text{~}Q(x) \text{ is true}) \implies (\text{~}P(x) \text{ is true}). $$

For the sake of brevity, I'm skipping a step here; though it is admittedly trivial.

Therefore,

$$ \tag{5} (1) \wedge (3) \implies \text{~}P(x) \text{ is true}. $$

Q.E.D.

EDIT:

So, to answer your questions:

You have this right.
For most purposes, you have no problem with assumptions.
Finally, you skipped a step between (3) and (4) in your post, which was made explicit by (2) in mine.

On a side note, for future reference, using $\LaTeX$ would probably be a better alternative to inserting mathematical notation in your posts on SE.

TIP: You can tag your equations by using "\tag{n}", where "n" denotes the number or string you want to tag your equation with.

I edited the 3rd list item, I had referred to the wrong lines. — ThisIsNotAnId, Apr 29 '12 at 17:37

score 0 · Answer 2 · edited Mar 09 '17 at 17:33

I apologize for being late to the game, but here goes:

$[(P\rightarrow Q)\wedge \sim Q] \rightarrow \sim P$

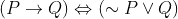Since $\\ (P\rightarrow Q) \Leftrightarrow (\sim P\vee Q)$ due to the identity rule, then 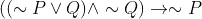$\\ ((\sim P \vee Q) \wedge \sim Q) \rightarrow \sim P$ . Now distribute 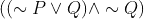$\\ ((\sim P \vee Q) \wedge \sim Q)$ to get $\\ ((\sim P \wedge \sim Q)\vee (Q \wedge \sim Q))$ .

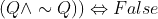$\\(Q \wedge \sim Q))$ is a contradiction, or a negation law. Thus $\\(Q \wedge \sim Q))\Leftrightarrow False$ .

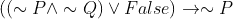So we now have $\\((\sim P \wedge \sim Q)\vee False) \rightarrow \sim P$ .

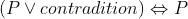we can now use the identity law of $\\ (P \vee contradition) \Leftrightarrow P$ , assuming 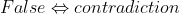$\\False \Leftrightarrow contradiction$ . Thus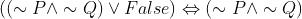 $\\((\sim P \wedge \sim Q) \vee False) \Leftrightarrow (\sim P \wedge \sim Q)$

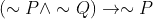$\\(\sim P \wedge \sim Q)\rightarrow \sim P$ is the definition of Decomposing a conjunction in the laws of Tautology. Please refer to page 7 of the following link: http://sites.millersville.edu/bikenaga/math-proof/truth-tables/truth-tables.pdf

Deriving Universal Modus Tollens

2 Answers2

Linked