1

Drawing with an example of what Im trying to do

I'm trying to make a sort of turtle program as a toy programming project. I can send instruction to go from A to B straight giving direction and distance and generating the needed cartesian point to draw the final image. But I need a method of telling the turtle to travel from B to C using a smooth curve, like in the example I drawn. A function will have to calculate a variable number of equidistant points (In the example, 5) from B to C sequentially. I only need to be pointed to the right mathematical formula... I will also like to be pointed to relevant material (websites, books) I can study to acquire the knowledge involved in this type of task. Thanks.

Vasily
  • 113

2 Answers2

1

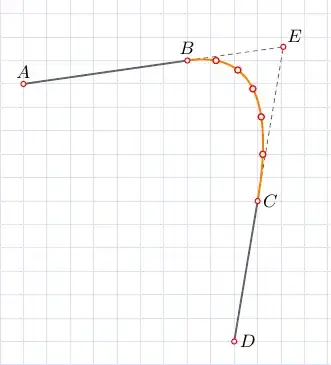
You gave a good example, but it is not clear what the general case is. It is also not clear what you mean by "smooth curve." In my answer I assume that by the latter you mean a curve with endpoints at $B$ and $C$, tangent vector at starting point $B$ parallel to vector $\overrightarrow{AB}$, and tangent vector at ending point $C$ parallel to vector $\overrightarrow{CD}$.

If your general case is where point $A$ is on the horizontal line through $B$ and to the left of $B$, point $D$ is on the vertical line through $C$ and below $B$, and point $C$ is down and to the right of $B$ at a $45°$ angle, a "smooth curve" is the quarter circle with center at $(x_a,y_c)$, and the $n$ points

$$(x_n,y_n)=\left( x_a+\cos\left[\frac{k\pi}{2(n+1)}\right] , y_c+\sin\left[\frac{k\pi}{2(n+1)}\right] \right)$$

for $k=1,2,\ldots,n$, and the angle in radians.

If your general case is the same but allows any angle from $B$ to $C$, then a good curve would be an ellipse. However, getting the points to be equidistant is much more difficult. You could approximate that by just using equal angle increments, as in my previous formulas (putting constants in front of the cosine and sine makes that an ellipse), but for a general ellipse that does not give equidistant points. You get a better approximation by using numerical methods to find the arc length of the ellipse arc and choosing the angles appropriately. For more on this, do a search for "arc length of an ellipse."

If your general case allows for any locations for your four points, you may want to use a Cubic Bézier curve. That will make a smooth curve, and this is the technique commonly used in car design and other graphing applications. Again, however, finding equidistant points will be a challenge. You probably could use the approximation by using equally spaced parameter $t$ values, and a better approximation by using numerical methods to find the arc lengths involved. For more information on this, just do a search for "Bezier curve" (I don't know if you should include the accent or not in your search terms).

Community
  • 1
Rory Daulton
  • 32,888
  • 6
  • 47
  • 64
1

Check out Bezier curves, they are a very popular choice for similar tasks in computer graphics.

For example, one way to do something similar in the turtle graphic project is to find point $E$ as the intersection of extensions of the segments $AB$, $DC$ and draw a quadratic Bezier segment, defined as

\begin{align} \mathcal{B}(t,P_0,P_1,P_2) &= P_0(1-t)^2+2P_1(1-t)t+P_2 t^2. \end{align}

While parameter $t$ changes from 0 to 1, the curve goes smoothly from $P_0$ to $P_2$.

enter image description here

But there is a cost for simplicity: points, generated using constant $\Delta t$ are not equidistant, but for a simple graphic project this may be not so important.

g.kov
  • 13,841