5

Information entropy is usually defined as

$$\text{I}_b({\bf p}) = -\sum_{\forall i}p_i\log_b(p_i)$$ i.e. the expected value of the negative logarithm of the probabilities.

This is all good when we have a finite set of outcomes i. This can also be estimated using a histogram, treating all values within each bin as the same outcome. Doing this will be possible if we are sampling from a continuous distribution and storing the outcome as floating point numbers. However the estimate we get will be dependent on how we create our histogram bins. It would be nice to get an estimate which is not dependent on how to build histogram bins but still gives a correct estimate for at least some important special cases.

Which methods or definitions do you think would be suitable to do this?

Update ("own work"): Consider the random variable $$X = \mathcal{N}(0,0.071) + U(1,n)\,\,\, \text{where the uniform}\,\,\, U(a,b) \in \{a,\cdots,b\}$$, and $\mathcal{N}(\mu,\sigma)$ is the normal distribution with mean $\mu$ and standard deviation $\sigma$.

Now we calculate some kind of a "similarity" or "adjacency" metric between all pair of samples as a monotonically decreasing function of some distance between the samples. In our example we experiment with $${\bf A}_{ij} = \exp\left[{-\frac{|x_i-x_j|^3}{s^3}}\right]$$ for some values of $s$.

Then we calculate the 8 largest eigenvalues of $\bf A$. These eigenvalues become very close to the number of samples in each Uniform bin.

$$\left[\begin{array}{l|llllllll}\text{eig}({\bf A})& 143.65&140.02&131.85&128.17&123.64&118.61&114.26&111.50\\f& 145&142&133&130&125&120&116&113 \end{array}\right] $$

If we normalize these (so they sum to 1) and calculate entropy, we get: $$\text{I}_2(\text{eig}{\bf A}) = 2.9946 \hspace{1cm} \text{I}_2(p) = 2.9948$$ Which both are very close to the theoretical entropy of 3 bits with 8 equiprobable states.

Could this maybe be used somehow?

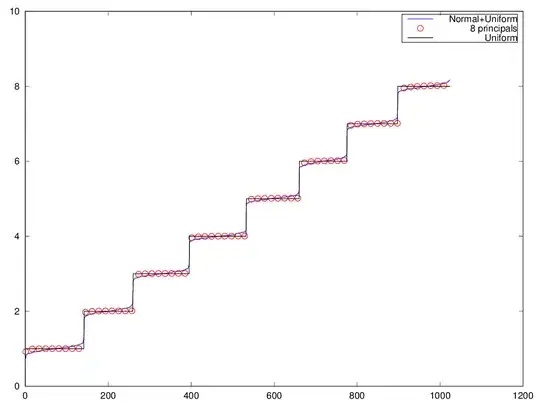
Below is a picture of sorted simulation (1024 samples) and the projection onto the 8 principal components:

Projection onto 8 Principal Components

mathreadler
  • 26,534
  • 1
    Wikipedia mentions two ways of extending information entropy to continuous case: the differential entropy, which is defined similarly to the finite case (for pdf $f$ $h[f] = - \int_{X} f(x) \ln f(x) dx$), but lacks some properties of entropy in finite case; and relative entropy, defined w.r.t. a reference measure $m$ as $\int_X f(x) \ln f(x) m(dx)$, where the distribution is assumed to be absolutely continuous w.r.t. $m$. – Budenn Jul 21 '15 at 10:41

1 Answers1

4

By rescaling the bins, you are changing the number of internal states, which shifts the origin of the entropy scale. That's actually the exact same problem classical thermodynamics has that only gets resolved in quantum theory, where the number of microscopic states is limited by the quantization of the phase space. When the absolute entropy scale is set, the planck constant appears in the expressions. The problem is that a continuum basically has infinite information capacity. The entropy differences, however, are still ok, if the bins are small enough to cover the details of the distribution and if your sample count is not too small (there are special theories that define entropy for small samples, which are very much in use in physics - for instance in particle physics, where sample rates can be extremely small, accurate statistical mechanics are essential).

If you want to know more, search for various thermodynamic definitions of entropy and any university grade textbook in the chapters about classical vs. quantum statistical dynamics.

orion
  • 16,154
  • 1
  • 34
  • 45
  • Thank you for the eye-opener. I remember a little bit of my statistical mechanics course, but it was some time ago. I suppose that one could make a similar quantization argument using the fact that a computer ultimately needs to quantize every number at some resolution no matter which application or field. – mathreadler Aug 15 '15 at 14:36