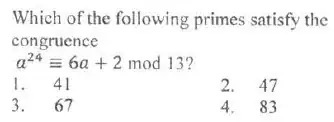
I don't have any clue . Can chinese remainder theorem can be used? I am studying number theory but I am not an expert as you can see. This question was set in the exam and I could not answer.
Asked
Active
Viewed 90 times
-3
-
Do you know Euler's Theorem? – João Ramos Jul 16 '15 at 16:24
-
1Hint: $a^{12}\equiv 1\pmod 13$ – Michael Galuza Jul 16 '15 at 16:25
-
1Chinese remainder is clearly not usable, $13$ is prime. Do you even know what CRT says? – Asinomás Jul 16 '15 at 16:35
-
See also here. $\ \ $ – Bill Dubuque Mar 07 '25 at 19:11
1 Answers
1
$a^{24}=(a^{12})^2\equiv 1^2\equiv 1 \bmod 13$ by Euler since $\varphi (13)=1$ as $13$ is prime.
From here you want $1\equiv 6a+2\iff 6a\equiv12\iff 66a\equiv132 \iff a\equiv 2 \bmod 13$.
Out of the primes listed only $41$ and $67$ satisfy this.
Asinomás
- 107,565
-
-
Thanks, thankfully I had a double mistake, so everything else is fine. – Asinomás Jul 16 '15 at 17:17
-
Two mistakes by chance landed at the correct answer. Not fine at all. And the step 66a(congruent to)132(mod 13) is totally redundant. – user118494 Jul 16 '15 at 17:26
-
how is it redundant? It's telling you the multiplicative inverse of $6\bmod 13$ is $11$. This is an important step. – Asinomás Jul 16 '15 at 17:32
-
It is redundant because 6a(congruent to) 12 (mod 13) directly implies that a(congruent to)2 (mod 13). as 13 is a prime . We did not need the inversion here. – user118494 Jul 16 '15 at 17:42
-
-
ok. 6a(congruent to) 12 (mod 13) is equivalent to saying 13 divides (6a-12)=6(a-2) . Now 13 being a prime and not dividing 6 , must divide a-2 . Thus a(congruent to)2(mod 13). That's a theorem about the primes. – user118494 Jul 16 '15 at 18:04
-