2

I'm defining Tensor Product as Berberian like $V_1\otimes V_2=\mathcal{L}(V_1^*,V_2)$ like here and inductively as $V_1\otimes V_2\otimes V_3=(V_1\otimes V_2)\otimes V_3$. I have defined the map $$\otimes:V_1\times\cdots\times V_n\rightarrow V_1\otimes\cdots\otimes V_n\\(x_1,\cdots x_n)\mapsto x_1\otimes\cdots\otimes x_n$$ Also inductively.

I've proven it's multilinear. I want to prove that for every vector space $U$ and every multilinear mapping $\nu:V_1\times\cdots\times V_n\rightarrow U$, there exists a unique linear mapping $S_\nu:V_1\otimes\cdots\otimes V_n\rightarrow U$ such that $\nu(x_1,\cdots,x_n)=S_\nu(x_1\otimes\cdots\otimes x_n)$.

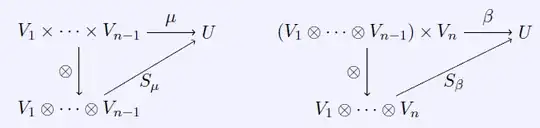
For $n=2$ we already have it. And if we suppose that $n>2$ and that for all $k<n $ there exists, then we have these two diagrams: enter image description here

where $\mu:V_1\times\cdots\times V_{n-1}\rightarrow U$ is multilinear (Of 1 degree below $\nu$) and $\beta:(V_1\otimes\cdots\otimes V_{n-1})\times V_n\rightarrow U$ is bilinear.

I want, for every $\nu$, to "separate" it in a way I can use these two diagrams to show the existence and uniqueness of $S_\nu$. So my 2 questions are:

  1. Is that possible?
  2. If it's not possible, How could I do it?
Community
  • 1
LeviathanTheEsper
  • 3,219
  • 1
  • 19
  • 40
  • Use $(x_1,\dotsc,x_n) = (x_1,\dotsc,x_{n-1},0) + (0,\dotsc,0,x_n)$ and multilinearity to factor $\mu$ through $(V_1 \otimes \dotsb \otimes V_{n-1}) \times V_n$. – A.P. Jul 11 '15 at 19:11
  • Humm, how? I could say $\mu(x₁,...,x_{n})=\mu(x₁,...,x_{n-1},0)+\mu(x₁,...,x_{n-1},x_{n})$, but it does not really get somewhere, $\mu(x₁,...,x_{n-1},0)=0$ and $\mu(x₁,...,x_{n-1},x_{n})$ is the same starting expression... – LeviathanTheEsper Jul 11 '15 at 23:38
  • No, you can say that $\mu(x_1,\dotsc,x_n) = \mu(x_1,\dotsc,x_{n-1},0) + \mu(0,\dotsc,0,x_n)$. In other words, you can define $\beta(x_1 \otimes \dotsb \otimes x_{n-1}, x_n) = S_{\mu \circ \iota}(x_1 \otimes \dotsb \otimes x_{n-1}) + (\mu \circ \gamma)(x_n)$, where $\iota$ and $\gamma$ are the injections of $V_1 \otimes \dotsb \otimes V_{n-1}$ and $V_n$ in $U$, respectively. – A.P. Jul 12 '15 at 09:48

0 Answers0