7

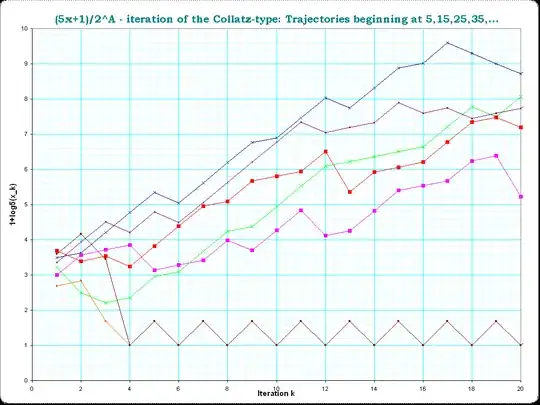
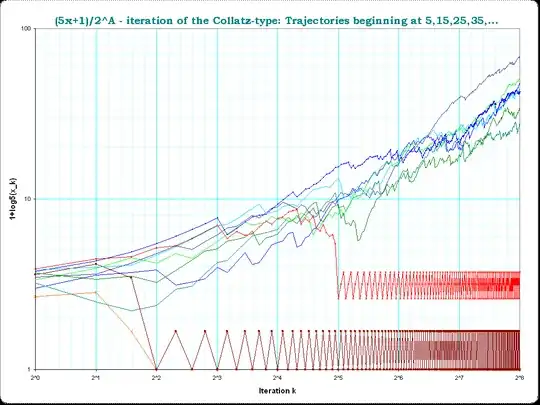
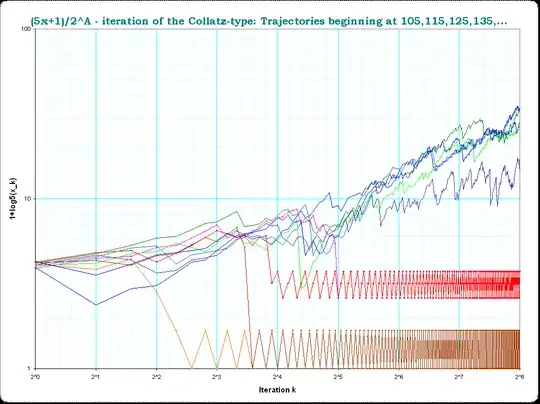
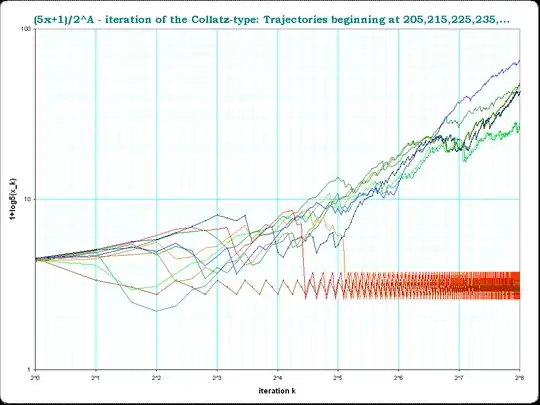
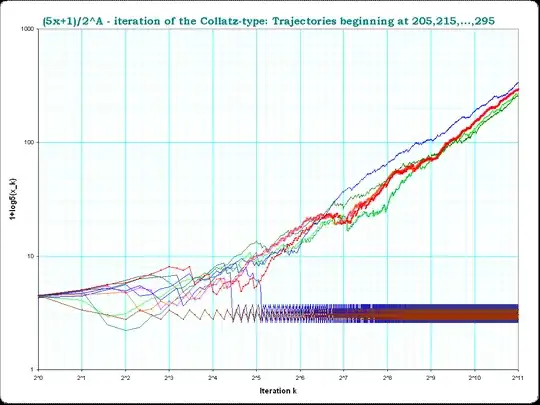
This is much like the $3x + 1$ iteration, except that if $x$ is odd, you do $5x + 1$ [and $\frac{x}{2}$ if $x$ is even]. If $x = 7$, then we have 7, 36, 18, 9, 46, 23, 116, 58, 29, 146, 73, 366, 183, 916, 458, 229, ...

I've iterated this twenty thousand times and found no power of 2. It's also possible that there is a period but it's so large that I'm not spotting it. And it's also possible that I have made a mistake somewhere along the way.

Surely someone else has also calculated this, even though $5x + 1$ is not as famous as $3x + 1$. I have tried other starting $x$ and seen that they quickly reach a period. Has anyone determined what happens with $x = 7$?

zyx
  • 36,077
Robert Soupe
  • 14,999
  • I don't quite get what you're asking. Why does it go from 36 to 18? And what is $3x+1$? Is this perhaps related to Collatz conjecture? :) –  Jul 06 '15 at 03:32
  • Is it possible a mistake? That is, have you iterated $20,000$ times by hand? – ajotatxe Jul 06 '15 at 03:33
  • 1
    I can't tell you what it does in the long term - I'd conjecture that the series starting there is a divergent trajectory (and hence never hits a power of 2 nor a cycle), but I ran 20,000 steps of the Tortoise and Hare Algorithm and found no cycle (nor a power of $2$ - so it doesn't hit one in the first $40,000$ steps at least) – Milo Brandt Jul 06 '15 at 03:36
  • This Collatz variation has been investigated before, although he didn't prove anything. – vadim123 Jul 06 '15 at 03:38
  • 2
    If I recall correctly, the $3x+1$ is carefully balanced between growing and shrinking if you assume $x$ is "random". One would then expect that $5x+1$ would have infinitely growing cases. – Ross Millikan Jul 06 '15 at 03:47
  • 4
    Working in Mathematica, one can compute this iteration to arbitrary length. Plotting this for 100,000(!) iterations, it seems that the sequence grows exponentially fast and without bound. (In order to speed up the iteration, I modified the odd case to use $x\mapsto (5x+1)/2$ and therefore skip a divide-by-two step.) – Semiclassical Jul 06 '15 at 03:52
  • @ajotatxe I used Javascript but only a thousand iterations at a time so that I could pinpoint the moment it switched over to scientific notation. – Robert Soupe Jul 07 '15 at 02:54

3 Answers3

7

In Lagarias' paper from 1985, he mentions (on the bottom of p. 12) this (5x+1) variation. He says that stochastic models predict that almost all orbits escape to infinity. However, this is a heuristic only; it was not proved (in 1985) that even a single orbit escapes to infinity. He calls this open problem (C3), on p. 22. This appears to remain open circa 2006, for here is a paper by Volkov, behind a paywall unfortunately, that continues study of this problem. Volkov gives three cycles, and computational (and heuristic) evidence that all other orbits diverge.

vadim123
  • 83,937
3

This is giving me some deja vu from centuries ago, but I don't know if it's because I actually found the answer and then forgot it. So I'm not sure if it reaches a period that has evaded detection by you and your colleages. I can tell you this much: it sure doesn't hit a power of $2$. Consider the sequence modulo $8$:

$$7, 4, 2, 1, 6, 7, 4, 2, 5, 2, 1, 6, 7, 4, 2, 1, \ldots$$

In order for this to hit a power of $2$, it would have to hit $4$ itself.

The Short One
  • 926
  • 1
  • 8
  • 27
  • Do you mean $8$ (i.e., $0$) itself? – Théophile Jul 06 '15 at 21:46
  • 1
    The "5", "2" in there shouldn't be there, right? @Théophile Periodicity mod $8$ shows that the sequence doesn't hit $8$ and it can't hit $2$ or $4$ without first htting $8$. – mrf Jul 06 '15 at 22:00
  • @mrf I get 7,4,2,1,6,7,4,2,5,2,1,6,7,4,2,5,2,5,2,1,6,7,4,6,7,4,6,7,4,6, suggesting he messed up a bit later (or maybe it was on purpose, can't be sure with that guy). I don't think 8 is the best modulus for this but I think the idea is on the right track. – Robert Soupe Jul 07 '15 at 02:58
  • @mrf I thought the line "it would have to hit 4 itself" referred to hitting 4 modulo 8, which it does, so I was confused. I now understand the wording. – Théophile Jul 07 '15 at 14:10
  • The idea is on the right track, but what is not properly explained is the fact that there is only one instance of $2^n \equiv 4 \pmod 8$, and that's $2^2 = 4$. – Bob Happ Jul 07 '15 at 14:27
  • 1
    How do you know that it never goes $6\mapsto3\mapsto0$? Knowing the even remainder of $n$ modulo $8$ won't tell you the remainder of $n/2$ modulo $8$. – Jyrki Lahtonen Apr 17 '19 at 11:44
1

this is a copy of an older answer on math.SE, see the duplicate question here. Your number has the number $35$ as pre-precedessor and its route can be seen on the pictures below.

Here are some pictures for your/our intuition. I graphed the trajectories for initial values $x=5,15,25,...$ for the first $256$ steps of $x_{k+1}=(5x_k+1)/2^A$.
To get the curves to a meaningfully visual interval I show logarithmic scales. The pictures show how most trajectories begin to diverge (not really a safe indication of what characteristic the infinite curves really have) but some show cycling already at early iteration indexes $k$ .

I find $2$ cycles besides the "trivial" one.

$x=5,15,25,35,...,95$ detail of the first few iterations . At the bottom we see the "trivial" cyle (brown curve):
picture
$x=5,15,25,35,...,95$ first $2^8 = 256$ iterations. At later iteration-indexes $k$ a first "non-trivial" cycle occurs (red line):
picture

$x=105,115,125,135,...,195$ first $2^8 = 256$ iterations .
picture

$x=205,215,225,235,...,295$ first $2^8 = 256$ iterations . Here a second "non-trivial" cycle becomes visible:
picture

$x=205,215,225,235,...,295$ first $2^{11} = 2048$ iterations
It seems really that all trajectories which are divergent up to iteration $k=256$ are also divergent up to iteration $k=2048$ . In general: I doubt that there are "later" cycles:
picture
Gottfried Helms
  • 35,815