The Platonic solids are best viewed as consisting of two families – those with triangular faces (the tetrahedron, the octahedron and the icosahedron), which for given edge count have maximal number of faces and minimal number of vertices, and their duals (the tetrahedron, the cube and the dodecahedron), in which three faces meet at each vertex and which for given edge count have maximal number of vertices and minimal number of faces. (The tetrahedron appears in both families because it's self-dual.)
For each of these families, we can derive a formula of the sort you're looking for. In both cases, we'll need the area and the solid angle of a regular polygon inscribed in a sphere. Consider a regular $N$-gon as consisting of $N$ triangles formed by its centre and the $N$ pairs of neighbouring vertices. Let $r$ be the distance from the centre to the vertices. Then each such triangle has area
$$\frac{r^2}2\sin\frac{2\pi}N\;,$$
and the $N$-gon has $N$ times that area. The solid angle $\Omega$ subtended by the triangle can be calculated from the dihedral angles of the tetrahedron it forms with the origin (see Wikipedia), namely as the excess over $\pi$ of the sum of the three dihedral angles at the origin. The calculation is a bit of a mess but leads to a nice result: If we want $n$ of these $N$-gons to subtend the solid angle $4\pi$ of the sphere, we need
$$
\sqrt{1-r^2}=\frac{\tan\left(\frac\pi N-\frac{2\pi}{Nn}\right)}{\tan\frac\pi N}\;.
$$
Solving this for $r$, substituting into the first equation and multiplying by $Nn$ to get the total area of the polyhedron yields
$$
\begin{eqnarray}
A(n,N)&=&\frac{Nn}2\left(1-\left(\frac{\tan\left(\frac\pi N-\frac{2\pi}{Nn}\right)}{\tan\frac\pi N}\right)^2\right)\sin\frac{2\pi}N\\
&=&\frac{Nn\cos^2\frac\pi N}{\tan\frac\pi N}\left(\tan^2\frac\pi N-\tan^2\left(\frac\pi N-\frac{2\pi}{Nn}\right)\right)\;.
\end{eqnarray}
$$
Now we can apply this to the two families of Platonic solids. For the first one, the one with triangles, we have $N=3$, and
$$
A_1(n)=A(n,3)=\frac{\sqrt3}4n\left(3-\tan^2\left(\frac\pi 3-\frac{2\pi}{3n}\right)\right)\;.
$$
For the three actual Platonic solids in this family, this yields
$$
\begin{array}{c|c|c|c}
n&\text{name}&A_1(n)&\simeq\\
\hline
4&\text{tetrahedron}&8\,/\sqrt3&4.6188\\
8&\text{octahedron}&4\sqrt3&6.9282\\
20&\text{icosahedron}&2\sqrt3\left(5-\sqrt5\right)&9.5745\\
\end{array}
$$
For the second family, we need to first determine $N$ as a function of $n$. In this family, three faces meet at each vertex, so the numbers $v$, $e$ and $f$ of vertices, edges and faces are given by $3v=Nn$, $2e=Nn$ and $f=n$, respectively. Then by Euler's polyhedron formula, $Nn/3-Nn/2+n=2$, so $N=6-12/n$. Thus, for this family we have
$$
\begin{eqnarray}
A_2(n)&=&A\left(n,6-\frac{12}n\right)\\
&=&\frac{6(n-2)\cos^2\left(\frac\pi6\frac n{n-2}\right)}{\tan\left(\frac\pi6\frac n{n-2}\right)}\left(\tan^2\left(\frac\pi6\frac n{n-2}\right)-\tan^2\left(\frac\pi6\frac n{n-2}-\frac\pi{3(n-2)}\right)\right)\;.
\end{eqnarray}
$$
For the three actual Platonic solids in this family, this yields
$$
\begin{array}{c|c|c|r}
n&\text{name}&A_2(n)&\simeq\\
\hline
4&\text{tetrahedron}&8\,/\sqrt3&4.6188\\
6&\text{cube}&8&8.0000\\
12&\text{dodecahedron}&2\sqrt{10\left(5-\sqrt5\right)}&10.5146\\
\end{array}
$$
Here's a plot of $A_1(n)$ (in blue), $A_2(n)$ (in red) and the area $4\pi$ of the sphere (in green):
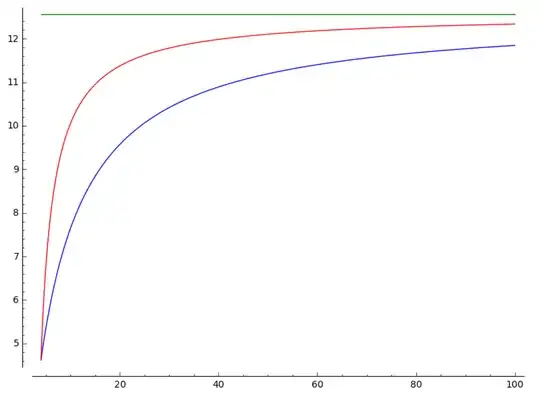
The second family, with maximal number of vertices and minimal number of faces for given edge count, converges much faster than the first, which is related to what Jim pointed out in a comment, that for the five Platonic solids taken together, the area increases with the number of vertices, not with the number of faces.
