9

Let $f(z)$ be holomorphic on the open disk $\mathbb{D} = \{z \in \mathbb{C}: |z| < 1\}$. Moreover, let $f$ be bounded on the boundary of $\mathbb{D}$, i.e. $$ \sup_{\varphi \in [0,2\pi]} |f(e^{i\varphi})| < \infty $$ (This class of functions is sometimes called $H^\infty$).

My question regards the boundary function $\tilde{f}(\varphi) := \lim_{r \rightarrow 1} f(r e^{i\varphi})$. Is it continuous?

User133713
  • 1,000

1 Answers1

10

It is not true in general that a bounded holomorphic function on the unit disk extends continuously to the boundary. This answer by Jonas Meyer explains how to construct such a function explicitly using Blaschke products.

However, if you believe the Riemann mapping theorem, there is a quick geometric way to construct a counterexample. Consider the following closed subset of the plane:

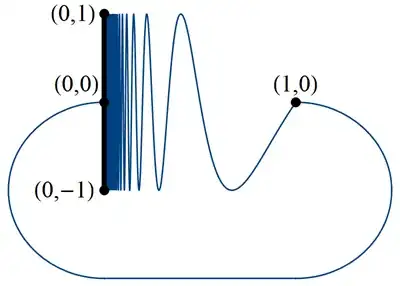
enter image description here

This is a variant of the famous topologist's since curve, and consists of the graph of $y = \sin(\pi/x)$ for $0<x<1$ together with the line segment from $(0,-1)$ to $(0,1)$ and a curve from the point $(0,0)$ to the point $(1,0)$.

Let $U$ be the interior region, i.e. bounded component of the complement of this closed set. Then $U$ is open and simply connected, so there exists a Riemann map $f\colon\mathbb{D} \to U$, where $\mathbb{D}$ is the open unit disk. The function $f$ is holomorphic and bounded, but $f$ cannot extend continuously to the boundary of the disk, since the boundary of $U$ isn't a continuous image of a circle.

Community
  • 1
Jim Belk
  • 50,794
  • 2
    In this example it is easy to see that the radial limit function is discontinuous, but for the general question I would just add that continuity of the radial limit function does not trivially imply continuity of the function on the closed disk. It is true, though, by the Luzin-Privalov theorems. – Lukas Geyer Jun 19 '15 at 13:17
  • Also, there is a function $(1+z)^{i}$, where $i=\sqrt{-1}$. It is bounded in the unit disk, without limit at $z=-1$. – AAK Jun 27 '22 at 07:54