I am trying to prove the following using complex analysis:
$$\sum_{n=-\infty}^{\infty}\frac{(-1)^{n}}{a^{2}+n^{2}}=\frac{\pi}{a\sinh(a\pi)}$$
I am told to use the following function:
$$f(z)=\frac{1}{(a^{2}+z^{2})\sin(\pi z)}$$
So we note that $f(z)$ has singularities at $z = \{\pm i a, n\}$, where $n \in \mathbb{Z}$. We can use the following contour (which I will call $\Gamma$):
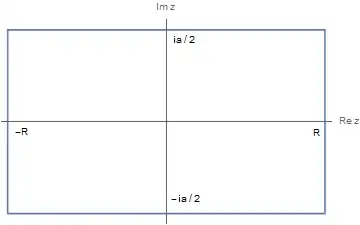
By Cauchy's Residue Theorem, we have:
$$\lim_{R \to \infty}\oint_{\Gamma}f(z)\:\mathrm{d}z=2\pi i \sum_{n=-\infty}^{\infty}\operatorname{Res}(n,f(z))$$
We can compute the residue at each point:
$$\operatorname{Res}(n,f(z))=\frac{(-1)^n}{\pi(a^{2}+n^{2})}$$
So we have:
$$\lim_{R\to \infty}\oint_{\Gamma}f(z)\:\mathrm{d}z = 2\pi i \sum_{n=-\infty}^{\infty}\frac{(-1)^{n}}{a^{2}+n^{2}}$$
But we have that:
$$\begin{align*}\lim_{R\to\infty}\oint_{\Gamma}f(z)\:\mathrm{d}z = \lim_{R\to\infty}\Bigg(I &+ \int_{-\frac{a}{2}}^{\frac{a}{2}}\frac{\mathrm{d}y}{(a^{2} + (R + iy)^{2}\sin(\pi(R + iy))} \\ &+ \int_{R}^{-R}\frac{\mathrm{d}x}{(a^{2} + (x + ia/2)^{2})\sin(\pi(x+ia/2))} \\ &+ \int_{\frac{a}{2}}^{-\frac{a}{2}}\frac{\mathrm{d}y}{(a^{2} + (iy - R)^{2})\sin(\pi(iy - R))}\Bigg)\end{align*}$$
However, I'm not not sure how to proceed? I'd be grateful for any hints!