I know what a 3x10 looks like, but I cannot seem to find a distinguishable pattern to extend it to a 3x14.
The 3x10 pattern I'm using looks like the one at the top right of figure 6 of this paper.
Any help would be greatly appreciated.
I know what a 3x10 looks like, but I cannot seem to find a distinguishable pattern to extend it to a 3x14.
The 3x10 pattern I'm using looks like the one at the top right of figure 6 of this paper.
Any help would be greatly appreciated.
Scwhenk's proof of necessary and sufficient conditions on $m,n$ for when there is a knight's tour on an $m \times n$ board is based on decomposing the board into a union of smaller boards, and has 9 base cases. You seem to want a way to "extend" a $3 \times 10$ tour into a $3 \times 14$ tour. The only obvious straightforward was to do this with Schwenk decomposition is to first tour the $3 \times 10$ and then tour the remaining $3 \times 4$. But $3 \times 4$ has no tour according to Schwenk's theorem. Thus it is unlikely, at least using the standard Schwenk decomposition approach naively, that you will be able to easily figure out how to do $3 \times 14$ by examining a single $3 \times 10$.
Compare:
$3\times10:$

$3\times12:$

$3\times14:$
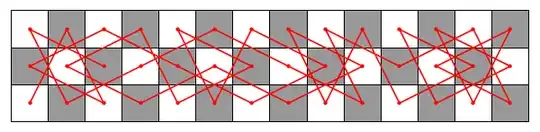
$3\times16:$
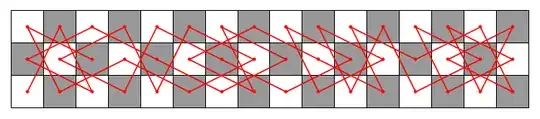
Note
These are not the only possible tours. There are $16, 176, 1536$ and $15424$ complete Hamiltonian cycles for $3\times10,12,14,16$ respectively.