I have been working on the indefinite integral of $\cos x/(1+x^2)$.
$$ \int\frac{\cos x}{1+x^2}\;dx\text{ or } \int\frac{\sin x}{1+x^2}\;dx $$
are they unsolvable(impossible to solve) or is there a way to solve them even by approximation?
Thank you very much.
There is no elementary antiderivative for either of those.
It's actually easier to deal with $e^{ix}/(1+x^2)$. As a corollary of a theorem of Liouville, if $f e^g$ has an elementary antiderivative, where $f$ and $g$ are rational functions and $g$ is not constant, then it has an antiderivative of the form $h e^g$ where $h$ is a rational function. For this to be an antiderivative of $f e^g$, what we need is $h' + h g' = f$.
Now with $f = 1/(1+x^2)$ and $g = ix$, the condition is $h' + i h = 1/(1+x^2)$. The right side has a pole of order $1$ at $x=i$. In order for the left side to have a pole there, $h$ must have a pole there, but wherever $h$ has a pole of order $k$, $h'$ has a pole of order $k+1$, so the left side can never have a pole of order $1$.
$\int\dfrac{\sin x}{1+x^2}dx$
$=\int\sum\limits_{n=0}^\infty\dfrac{(-1)^nx^{2n+1}}{(2n+1)!(x^2+1)}dx$
$=\int\sum\limits_{n=0}^\infty\dfrac{(-1)^nx^{2n}}{2(2n+1)!(x^2+1)}d(x^2+1)$
$=\int\sum\limits_{n=0}^\infty\dfrac{(-1)^n(x^2+1-1)^n}{2(2n+1)!(x^2+1)}d(x^2+1)$
$=\int\sum\limits_{n=0}^\infty\sum\limits_{k=0}^n\dfrac{(-1)^nC_k^n(-1)^{n-k}(x^2+1)^k}{2(2n+1)!(x^2+1)}d(x^2+1)$
$=\int\sum\limits_{n=0}^\infty\sum\limits_{k=0}^n\dfrac{(-1)^kn!(x^2+1)^{k-1}}{2(2n+1)!k!(n-k)!}d(x^2+1)$
$=\int\left(\dfrac{1}{2(x^2+1)}+\sum\limits_{n=1}^\infty\sum\limits_{k=0}^n\dfrac{(-1)^kn!(x^2+1)^{k-1}}{2(2n+1)!k!(n-k)!}\right)d(x^2+1)$
$=\int\left(\dfrac{1}{2(x^2+1)}+\sum\limits_{n=1}^\infty\dfrac{1}{2(2n+1)!(x^2+1)}+\sum\limits_{n=1}^\infty\sum\limits_{k=1}^n\dfrac{(-1)^kn!(x^2+1)^{k-1}}{2(2n+1)!k!(n-k)!}\right)d(x^2+1)$
$=\int\left(\sum\limits_{n=0}^\infty\dfrac{1}{2(2n+1)!(x^2+1)}+\sum\limits_{n=1}^\infty\sum\limits_{k=1}^n\dfrac{(-1)^kn!(x^2+1)^{k-1}}{2(2n+1)!k!(n-k)!}\right)d(x^2+1)$
$=\int\left(\dfrac{\sinh1}{2(x^2+1)}+\sum\limits_{n=1}^\infty\sum\limits_{k=1}^n\dfrac{(-1)^kn!(x^2+1)^{k-1}}{2(2n+1)!k!(n-k)!}\right)d(x^2+1)$
$=\dfrac{\sinh1\ln(x^2+1)}{2}+\sum\limits_{n=1}^\infty\sum\limits_{k=1}^n\dfrac{(-1)^kn!(x^2+1)^k}{2(2n+1)!k!k(n-k)!}+C$
If you take
$$f(z) = \frac{e^{iz}}{1+z^2}$$
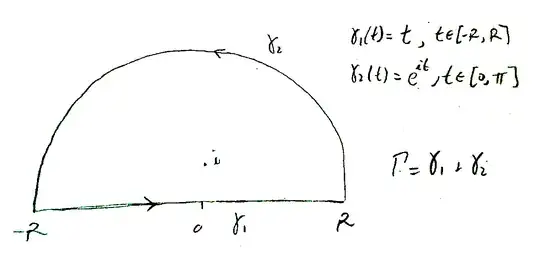
and apply the residue theorem over the path $\Gamma = \gamma_1 + \gamma_2$:
$\Gamma$" />
You have as follow:
$$\frac{1}{2\pi i}\int_{\Gamma} f(z)dz = \text{Res}(f,i)$$
'cause, of the two poles of $f(z)$, only $i$ is inside $\Gamma$. So, $\int_{\Gamma} f(z)dz = \int_{\gamma_1} f(z)dz + \int_{\gamma_2} f(z)dz$. Let's do it one by one:
$$\int_{\gamma_1} f(z)dz = \int_{\gamma_1} \frac{e^{iz}}{1+z^2}dz = \int_{-R}^{R} \frac{e^{it}}{1+t^2}dt$$
because we have parametrized $\gamma_1$ as $\gamma_1(t) = t$, for $t\in[-R,R]$ and $dz = dt$.
$$\int_{-R}^{R} \frac{e^{it}}{1+t^2}dt = \int_{-R}^{R} \frac{\cos(t) + i\sin(t)}{1+t^2}dt = \int_{-R}^{R} \frac{\cos(t)}{1+t^2}dt + i\int_{-R}^{R} \frac{\sin(t)}{1+t^2}dt$$ But the second one of this two integrals is zero, cause $\frac{\sin(t)}{1+t^2}$ is an odd function. Allright, let's take care of the integral
$$ \int_{\gamma_2} f(z)dz = \int_{0}^{\pi} \frac{e^{iRe^{it}}}{1 + R^2e^{i2t}}iRe^{it} dt $$
'cause, now, $\gamma_2 = e^{it}$ for $t \in [0,\pi]$, so $z=Re^{it}$ and $dz = iRe^{it}dt$. Then, we have:
$$ \int_{0}^{\pi} \frac{e^{iRe^{it}}}{1 + R^2e^{i2t}}iRe^{it} dt = \int_{0}^{\pi} \frac{e^{iR(\cos(t)+i\sin(t))}}{1 + R^2e^{i2t}}iRe^{it}dt =\\ \int_{0}^{\pi} \frac{e^{iR\cos(t)} e^{-R\sin(t)}}{1 + R^2e^{i2t}}iRe^{it}dt \leq \int_{0}^{\pi} \left|\frac{e^{iR\cos(t)} e^{-R\sin(t)}}{1 + R^2e^{i2t}}iRe^{it}dt\right| = \int_{0}^{\pi} \frac{R}{1 + R^2e^{i2t}}e^{-R\sin(t)}dt $$ and, $$ \lim_{R\rightarrow +\infty} \int_{0}^{\pi} \frac{R}{1 + R^2e^{i2t}}e^{-R\sin(t)}dt = 0 $$
So, summing up, we have
$$ \int_{\Gamma} f(z)dz = \int_{-R}^{R} \frac{\cos(t)}{1+t^2}dt $$
and, trivially,
$$ \lim_{R\rightarrow +\infty} \int_{-R}^{R} \frac{\cos(t)}{1+t^2}dt = \int_{-\infty}^{\infty} \frac{\cos(t)}{1+t^2}dt $$
just, what we want to know. The computing of Res($f, i$) it's simple 'cause $i$ is a pole of degree 1, so you just have to derive the denominator and evaluate all in $z=i$, And finally, for the residue theorem, we have, for $R\rightarrow +\infty$:
$$ \frac{1}{2\pi i} \int_{\Gamma} f(z)dz = \frac{1}{2\pi i} \int_{-\infty}^{\infty} \frac{\cos(t)}{1+t^2}dt = Res(f, i) = \frac{e^{it}}{(1+z^2)'}\Bigg\rvert_{z=i} = \frac{e^{it}}{2z}\Bigg\rvert_{z=i} =\frac{e^{-1}}{2i}\\ \longrightarrow \int_{-\infty}^{\infty} \frac{\cos(t)}{1+t^2}dt = \frac{\pi}{e} $$
