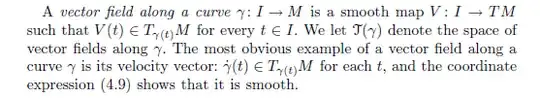Let $γ : I→R^3$ be a regular parametrization of a curve C. If asked what a vector field on C is I would perhaps answer like this:
1) "a smooth function $v$ associating to any point $γ(t)$ of C an element of the tangent space of $R^3$ at $γ(t)$".
An alternative answer: 2) "a smooth function $f$ associating to any t $∈$ I an element of the tangent space of $R^3$ at $γ(t)$".
My question: is the second answer technically wrong? Thanks.