This is not a complete answer. I did some progress and convert the surface integral into an improper double integral. So anyone willing to find a solution may use the final result in this post.
Your surface for $a=1$ and ratio $1:1:1$ between the $x$, $y$, and $z$ axis looks like this
$\qquad \qquad \qquad \,\,$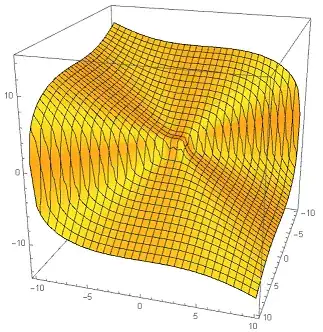
so it is not a closed surface and we cannot use the divergence theorem as it was mentioned in the comments too. Next, note that
$$\begin{array}{}
g(x,y,z)=x^3+y^3+z^3-a^3 \\
{\bf{F}} = \frac{\bf{x}}{\left\| {\bf{x}} \right\|}= {x\over \sqrt{x^2+y^2+z^2}}{\bf{i}} + {y\over \sqrt{ x^2+y^2+z^2}} {\bf{j}} + {z\over \sqrt{x^2+y^2+z^2}} {\bf{k}} \\
{d\bf{S}}= {1 \over {\partial{g} \over \partial z}} \nabla g \, dx dy \\
{1 \over {\partial{g} \over \partial z}}\nabla g=\frac{1}{z^2}(x^2 {\bf{i}} + y^2 {\bf{j}} + z^2 {\bf{k})} \\
{\bf{F}} \cdot {d\bf{S}} = \frac{x^3+y^3+z^3}{z^2 \sqrt{x^2+y^2+z^2}} dx dy = \frac{a^3}{z^2 \sqrt{x^2+y^2+z^2}} dx dy\\
\end{array}$$
and finally the surface integral becomes
$$\iint_{S} {\bf{F}} \cdot {d\bf{S}} = \int_{x=-\infty}^{+\infty} \int_{y=-\infty}^{+\infty} \frac{a^3}{z^2 \sqrt{x^2+y^2+z^2}}dydx \tag{*}$$
and note that $z$ is a function of $x$ and $y$ by the relation
$$z=(a^3-x^3-y^3)^{\frac{1}{3}}$$
Now, one may work on $(*)$ to obtain some result.
