Outer solution
Since $ε$ represents an infinitesimal scale and thus $ε^{-1}$ a level of infinity, then for points where $y(x), y'(x),y''(x)\ll ε^{-1}$ are of "normal" size the equation reduces to the outer form
$$
y(x)·(y'(x)-1) = O(ε)
$$
and thus either $y(x)=0+O(ε)$ or $y'(x)=1+O(ε)$ which implies $y(x)=C+x+O(ε)$. To satisfy one of the right boundary one would one of the following variants for the outer solution:
$$
y_{outer}(x)=0,\\
y_{outer}(x)=x,\\
y_{outer}(x)=2+x.
$$
with a jump at the boundary with the violated solution or possible in-between connecting two suitable outer solutions.
Inner solution
At any point $x_0$ not satisfying the "appreciable boundedness" condition for function value and derivatives, one has to consider a local parametrization $x=x_0+δX$. Let $Y(X)=y(x_0+δX)$, then the differential equation becomes
$$
εY''(X)+δ(Y'(X)-δ)Y(X)=0.
$$
It is assumed that this parametrization restores the "appreciable boundedness" for $Y,Y',Y''$. The infinitesimal scale coefficients of the term in this equation are $ε,δ,δ^2$. To get a non-trivial equation from the dominating terms one needs two dominant scale coefficients of equal magnitude. The only case to consider here is $ε\sim δ\gg δ^2$. Use for nicer equations $δ=2ε$, then the reduced equation is
\begin{align}
&&Y''(X)+2Y(X)Y'(X)&=0
\\ &\implies&
Y'(X)+Y(X)^2 &= Y'(0)+Y(0)^2=a^2
\\ \\ &\implies&
Y(X)&=a·\tanh(a·(X-C))~~\text{ or }~~ Y(X)=a·\coth(a·(X-C))
\end{align}
(a negative integration constant gives unbounded solutions). In the case $|Y(0)|<a$ the first solution applies and $y(x)=Y((x-x_0)/(2ε))$ changes in the interval $(x_0-\sqrt{ε},x_0+\sqrt{ε})$ (or any other interval width $O(ε^{1-α})$, $0<α<1$) from $-a$ to $a$ crossing the $x$ axis at $x=x_0+2εC$. The second solution form would represent a downward jump which is not relevant here as the given boundary conditions require an upward jump.
None of the outer solutions take negative values, so it is impossible to have the boundary layer at an inner point or at the right boundary. At the left boundary a jump from $0$ to $2$ is possible with $a=2$, $C=0$ and thus the inner solution
$$
y_{inner}(x)=2·\tanh\left(\frac{x}{ε}\right)
$$
and a combined approximation
$$
y_{approx}(x)=y_{inner}(x)+y_{outer}(x)-y_{outer}(0)=2·\tanh\left(\frac{x}{ε}\right)+x.
$$

Variations
Were the given boundary conditions, as example, $y(0)=-3$ and $y(1)=3$, then one would need the jump to be inside the interval connecting $-3+x$ and $2+x$ at a point $x_0$ where $-(-3+x_0)=3-x_0=2+x_0$, that is $x_0=\frac12$ with $a=\frac52$. The approximate solution would then be
$$
y_{approx}(x)=x-\frac12+\frac52·\tanh\left(\frac5{4ε}\left(x-\frac12\right)\right)
$$
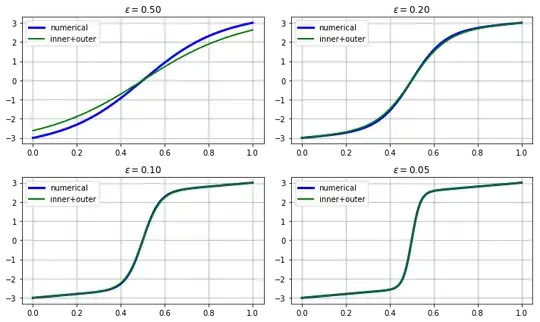
For general $y(0)=A<0<B=y(1)$, the same as above applies if $x_0=-\frac{A+B-1}2$ is well inside the interval $(0,1)$.
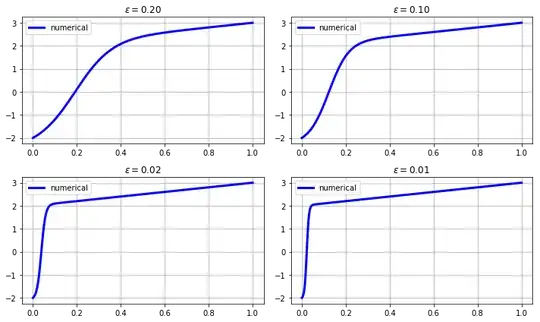
It not as straightforward to find an approximate solution if the boundary conditions do not fall into one of the above scenarios. For instance for the boundary conditions $y(0)=-2$, $y(1)=3$ one would need a jump from $-2$ to $2$ at $x_0=0$. The numerical solution indicates an incomplete jump at about $x_0=ε$ from $-2$ to around $a=2+ε$.