Approximate solution of differential equation

Question

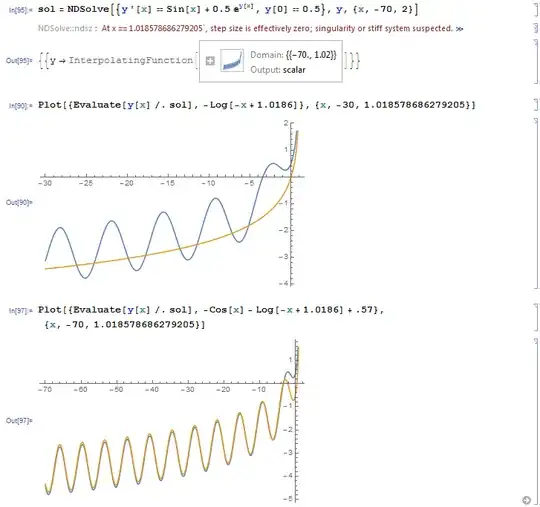
My task: find approximate solution as $$y = y_0(x) + y_1(x)\lambda + y_2(x)\lambda^2 + y_3(x)\lambda^3$$ of differential equation $$y' = \sin x + \lambda e^y, y(0)=1-\lambda. \ \ \ \ (*)$$ My attempt :

Let $$y(x,\lambda) = y_0(x) + y_1(x)\lambda + y_2(x)\lambda^2 + y_3(x)\lambda^3.$$ Then $$ y_0(x) = y(x,0)$$ $$y_1(x) =\frac{ \partial y(x,\lambda)}{\partial \lambda}_{\lambda = 0}$$ $$y_2(x) =\frac{1}{2}\frac{ \partial^2y(x,\lambda)}{\partial \lambda^2}_{\lambda = 0}$$ $$y_3(x) =\frac{1}{6}\frac{ \partial^3y(x,\lambda)}{\partial \lambda^3}_{\lambda = 0}$$

And

$$ y_0'(x) = y'_x(x,0)$$ $$y_1'(x) =\frac{ \partial}{\partial \lambda}y'_x(x,\lambda)_{\lambda = 0}$$ $$y_2'(x) =\frac{1}{2}\frac{ \partial^2}{\partial \lambda^2}y'_x(x,\lambda)_{\lambda = 0}$$ $$y_3'(x) =\frac{1}{6}\frac{ \partial^3}{\partial \lambda^3}y'_x(x,\lambda)_{\lambda = 0}$$

After that, using (*), i got $$y_0'(x)= sin x$$ $$y_1'(x)=e^{(y_0)}$$ $$y_2'(x)=e^{(y_0)}y_1;$$ $$y_3'(x)=e^{(y_0)}(y_1^2+y_2)$$ And i stopped here. There isn't a solution in these integrals. Maybe, there is another solution of my task? Thanks

Answer 1

I don't know if you prefer the exact solution instead of approximates. Infortunately, the analytic expression includes an integral $\int e^{-\cos(x)}dx$ which has no standard closed form :

Note that $y(x)=-\cos(x)-\ln(f(x)+C)$

where $f(x)$ is the function as shown above. This is consistent with the previous answer from grdgfgr.

For numerical calculus, there is no difficulty to compute accurate values of the integral, then accurate numerical values of the whole function $y(x)$.

If you want good approximates on the form of formula, it is possible to express $\int_0^x e^{-\cos(t)}dt$ on the form of finite series.

Ultimately, the integral can be remplaced by the next Fourier series : $$\int_0^{x} e^{-\cos(t)}dt=a_0x+\displaystyle\sum_{n=1} \frac{a_n}{n}\sin(nx)$$ $a_0=1.266066$

$a_1=-1.130318$

$a_2=0.271495$

$a_3=-0.0443368$

$a_4=0.00547424$

$a_5=-0.000542926$

It is sufficient to make negligible the deviations.

Answer 2

The solution is easier than you may think at first glance.

Just expand the solution of the differential equation into Taylor series.

$$y＝y(0)+\frac{y'(0)}{1!}x+\frac{y''(0)}{2!}x^{2}+...$$

The coefficients $y'(0),y''(0)$, etc. we can evaluate directly from the differential equation by differentiating it. Some of the first coefficients:

$$y(0)=1-\lambda$$

$$y'(0)=\lambda e^{1-\lambda}$$

$$y''(0)=1+\lambda^{2} e^{2(1-\lambda)}$$

$$y'''(0)=\lambda e^{1-\lambda}\left [1+2\lambda^{2} e^{2(1-\lambda)}\right ]$$

Now, after you've put these results into the Taylor series, all you need is to regroup the series terms to separate terms that contain only $\lambda,\lambda^{2},\lambda^{3}$ etc.

Answer 3

I am afraid my solution will not help you with your homework. If I were you, I would ask the teacher/TA since this seems like a weird question to me. But I still think it is an interesting approach and it is good to know such approaches are possible.

Lets try to find an asymptotic solution to this equation to have an understanding of how it behaves. Let's assume sinx is negligible compared to $y'$ and $e^y$. In that case, the solution becomes $-log(-x+c)$. Consider $x$ values close to $c$. It makes both $y$ and $e^y$ infinity, and sinx is negligible compared to infinity.

Just for fun, lets compare this to the numerical solution of the equation:

The general solution appears to be of the form:

$$-cos(x)-log(-x+d)+c$$

where $d$ is the position of the singularity and $c$ should be determined using an initial condition y(x<-10) (y(0)cannot be connected to the actual solution as you can see from the graph)

Evidently, it is going to be very difficult to approximate such a solution using any continuous function.

Getting back to how you might actually solve your question as it was intended: If this is an approximation assignment, why don't you approximate $\int e^{-cost}$ using taylor expansion?

$\int e^{-cost} \sim 1.0128527022016056\int(\frac{\cos ^2(x)}{2}-\cos (x)+1)dx $

Unfortunately you need some multiplicative factoring for the approximation to remain valid for a large interval.