Finding a point on Archimedean Spiral by its path length

Question

I've been curious about Archimedean Spirals and their relations to Sacks Spirals and prime numbers.

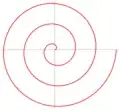
enter image description here

I would like to draw some visualizations of the points with a given distance from the center, across the spiral path. Is there a formula for that?

Clarification:

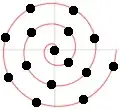
enter image description here

I'm looking for a function that, given a distance along the path, fives the coordinates of a point along that path.

Consider the example image above. $f(0)=(0,0)$, because a distance of 0 along the path is the origin of axis. In this (rough) sketch, $f(1)≃(1, -3)$, $f(2)≃(0.8, 1.1)$, $f(3)≃(-1.3, 1.1)$ and so on.

Thanks a lot for your help!

It's a slight variation of that link, which is actually quite useful and interesting. I apologize for not being clear. — Adam Matan, Apr 05 '12 at 06:52

score 5 · Answer 1 · edited Apr 13 '17 at 12:21

5

The arc length for $r=a\theta^{1/n}$ is given by $$ s(\theta)=a\theta^{1/n} {_2F_1}\left(-\frac{1}{2},\frac{1}{2n}; 1+\frac{1}{2n}; -n^2\theta^2\right), $$ where $_2F_1(a,b;c;x)$ is a hypergeometric function. See here.

For $n=1$ (your case) this boils down to $$ \frac{a}{2}\left[\theta\cdot\sqrt{1+\theta^2}+\ln \left(\theta+\sqrt{1+\theta^2} \right)\right]. $$

You get there by using $\vec r= (a\cdot \theta\cdot\cos\,\theta,a\cdot \theta\cdot\sin\,\theta)$ and the formula for the arc length $$ \begin{eqnarray} s(\theta)&=&\int_{0}^{\theta} \sqrt { [r_x'(\varphi)]^2 + [r_y'(\varphi)]^2 }\, d\varphi\\ &=&\int_{0}^{\theta} \sqrt {1+x^2} \, dx .\\ \end{eqnarray} $$ You'll find some ways to solve similar things like the last integral here.

edited Apr 13 '17 at 12:21

Community

1

answered Mar 29 '12 at 21:28

draks ...

18,755

+1 Thanks! How do I use this formula to find the (x, y) or (r, θ) coordinates of a points whose distance from the center is given? – Adam Matan Apr 01 '12 at 10:33
@AdamMatan In polar coordinates this is pretty easy: $(a\theta,\theta)$. Cartesian is left to you as an exercise... – draks ... Apr 01 '12 at 17:33
1

I can easily convert polar to Cartesian coordinate and vice versa. The part that I'm missing is the equation where s (arc length) is the input, and a coordinate is calculated from it. Doesn't your formula go the other way around? – Adam Matan Apr 01 '12 at 17:48
@AdamMatan hm, but then you would have to invert the formula for $s$...I'm not sure, if this will work. – draks ... Apr 01 '12 at 17:58
So how would you recommend drawing something like this: http://en.wikipedia.org/wiki/File:Sacks_spiral.svg ? traverse along the path in very small steps and accumulate the distance passed so far? – Adam Matan Apr 01 '12 at 19:08
@AdamMatan Just to get you right: You want something like $s^{-1}(n^2-n+41)=\theta$? – draks ... Apr 02 '12 at 08:41
Thanks a lot for your efforts. How do I get the coordinates from the distance using such function? – Adam Matan Jul 25 '12 at 17:31
Hey @AdamMatan you might have a look at this one: How to place objects equidistantly on an Archimedean spiral? – draks ... Feb 06 '13 at 19:35

score 0 · Answer 2 · edited Apr 13 '17 at 12:21

The answer should be quite clear given the post above. All you need to do is to find the inverse function of that

$$ s(\theta)=\frac{P}{2\pi}[\frac{\theta}{2}\sqrt{1+\theta^{2}}+\frac{1}{2}\ln(\theta+\sqrt{1+\theta^{2}})] $$

where P is pitch length. Once you get $\theta(s)$, you can find $x(\theta)$ and $y(\theta)$ fairly easily.

If you can't solve $\theta(s)$ analytically, you solve it numerically. As given in the comment of the previous post, you may have a look at this one:

How to place objects equidistantly on an Archimedean spiral?

Finding a point on Archimedean Spiral by its path length

2 Answers2