10

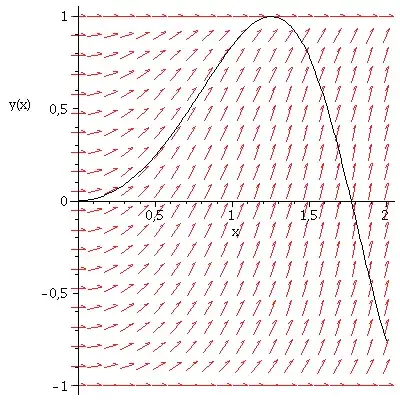
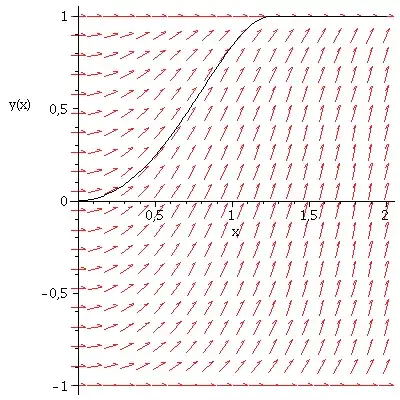
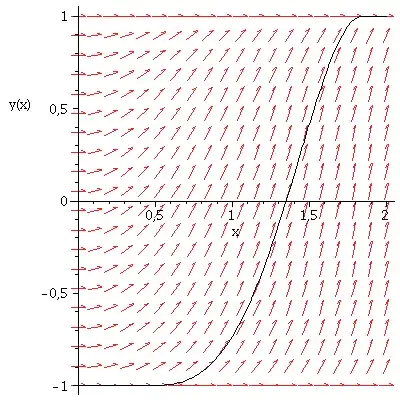
In most introductory ODE textbooks we can find the following definition:

A separable first-order ODE is the one of the form $$y'=g(x)h(y)$$ and if $h(y)\neq0$, then the general solution is found by integration (using chain rule). Next, we must find every $y_0$ such that $h(y_0)=0$ and the constant function $y=y_0$ satisfies the above ODE (called singular solutions).

I'm trying to learn this method in a rigorous way by using the existence and uniqueness of solution theorems and adding restrictions over $g$ and $h$, but can't deal with the following:

Does there exist a solution $f$ defined in some $A\in \mathbb{R}$ such that there exists $x_0\in A$ such that $h(f(x_0))=0 $ but $f$ is not constant? I mean, if $f(x_0)=y_0$, then $h(y_0)=0$, so we can't divide by $h(y)$ and integrate using separable equation method. I know that $f(x)=y_0$ is a solution, but what can we say about a non-constant $f/f(x_0)=y_0$?

Also, can you recommend books explaining this kind of solving-ODE's methods but in an absolutely rigorous way?

EDIT: This edit is made after the bounty (I thought it was implicit in the spirit of the question, but maybe I couldn't state it properly due to my lack of expertise in english), but I'd really want to know what further hypothesis need to be given in order to assure that every singular solution must be constant.

Any help is highly appreciated. Thanks and regards

nmasanta
  • 9,640
Ab urbe condita
  • 363
  • 1
    Concerning your last question: a sufficient condition to ensure that the only singular solutions are constants is Lipschitz continuity of the function $h$. This condition makes the standard uniqueness theorem available and prevents the merging of multiple solutions shown in my answer below. – Giuseppe Negro Apr 20 '15 at 09:47

1 Answers1

15

Yes, you might have solutions that are not constant and such that $h(y)=0$ somewhere.

Here's an example I ran across on a textbook some years ago: \begin{equation} \tag{1} \frac{dy}{dx}=2x(1-y^2)^{1\over 2}. \end{equation} You have the constant solutions $y=\pm 1$. If you carelessly separate variables you get $$ \int\frac{dy}{(1-y^2)^{1\over 2}} = \int 2x\, dx $$ from which you obtain the "general integral" $$ \tag{!!} y(x)=\sin(x^2+C). $$ This is the solution I found on the textbook. Problem is, it is wrong. Take for example $C=0$. The function $\sin(x^2)$ is oscillating, so its first derivative changes sign infinitely often for $x\ge 0$. And as you can see from (1), the derivative $\frac{dy}{dx}$ must be nonnegative on the whole half-line $[0, \infty)$.

To understand what is going on let us observe the graph of $\sin(x^2)$ on the phase field of (1): enter image description here

The black line matches with the phase field until it touches the critical level $y=1$. Then it goes amiss. The correct solution is the following:

Correct Solution to (1)

As soon as the solution touches the critical level, it merges with the constant solution. The general solution to the Cauchy problem \begin{equation} \begin{cases} y'=2x(1-y^2)^{1\over 2},& x> 0\\ y(0)=y_0\in (-1, 1] \end{cases} \end{equation} is the following: \begin{equation} y(x)= \begin{cases} \sin(x^2+\arcsin y_0), & x<\sqrt{\frac{\pi}{2}-\arcsin(y_0)} \\ 1, & x\ge \sqrt{\frac{\pi}{2}-\arcsin(y_0)} \end{cases} \end{equation} For $y_0=-1$ you have infinite solutions. One is the constant one $y(x)=-1$, the others are pictured below:

General Solution to (1)

The analytical expression of those solutions is the following: \begin{equation} y_{x_0}(x)= \begin{cases} -1, & x<x_0 \\ \sin\left(x^2-x_0^2-{\pi\over 2}\right), & x_0\le x < \sqrt{x_0^2+\pi} \\ +1, & \sqrt{x_0^2+\pi}\le x. \end{cases} \end{equation} The parameter $x_0\ge 0$ is the abscissa of the point in which the solution leaves the critical line $y=-1$.

Giuseppe Negro
  • 34,508
  • P.S.: This example comes from this discussion on another mathematical forum (in Italian). – Giuseppe Negro Apr 19 '15 at 20:18
  • 1
    Great answer! Unfortunately it implies that every book I know about is wrong, at least without further hypothesis. So, what can I do? I mean, does there exist at least one book/lecture notes where I can learn this topic properly? The more advanced textbooks such as Coddington and Levinson don't even care about those methods of solving... – Ab urbe condita Apr 19 '15 at 21:05
  • 2
    @CABJ: I am glad you liked this answer (you could upvote and/or accept it if you like). Regarding the books, the problem here is that you have a failure of the uniqueness theorem, due to the fact that $(1-y^2)^{1\over 2}$ is not Lipschitz continuous near $y=\pm 1$. This produces the merging of multiple solutions shown above. But when you are Lipschitz continuous in $y$ (and that's almost always the case, in practice), you can separate variables without much worrying. – Giuseppe Negro Apr 19 '15 at 21:41
  • 3
    Even in this example, one could have avoided the error if one had integrated with more care: $$ \int_{y_0}^y \frac{dy'}{(1-(y')^2)^{1\over 2}} = \int_{0}^x 2x', dx',\qquad \lvert y(x)\rvert<1$$ taking into account that the function that one finds might cease to be a valid solution if touches the singular values $y=\pm 1$. That's because in that case one is dividing by zero in the equation (1). This integration correctly produces the local solutions $y(x)=\sin(x^2+\arcsin y_0)$, valid only for small $x$ (see the main text). – Giuseppe Negro Apr 19 '15 at 21:51
  • Now I'm starting to understand what's behind all this. One more doubt: when you find the general solution, did you rely on the graph to write the final expression or could you find it analytically? I mean, without looking at the phase field, how do you know there aren't any other solutions? If it's already done in the answer, tell me and I'll get it later while reading with more care. – Ab urbe condita Apr 19 '15 at 22:03
  • @CABJ: I looked at the phase field since it was easy to picture. To rigorously prove that there are no more solutions one needs to do some qualitative analysis. See this book, for example. In the present case one may reason as follows: since we have uniqueness in the strip $\lvert y\rvert<1$, integral curves cannot cross there. They can cross at the critical levels $\lvert y \rvert =1$, but as soon as they leave, they enter the non-critical region. Therefore they must agree with the unique local solutions given by the explicit integration.. – Giuseppe Negro Apr 20 '15 at 09:41
  • ... and this shows that all solutions must be the pasting of constant solutions at the critical level and local solutions of the form $\sin(x^2+C)$. – Giuseppe Negro Apr 20 '15 at 09:42
  • @CABJ: You are welcome. – Giuseppe Negro Apr 22 '15 at 12:53