I want to geometrically prove that $\cos(\pi-\phi)=-\cos\phi$ without resorting to the unit circle or trigonometric formulas, but have difficulties figuring it out.
It's easy enough to do the sine, however: you draw a right triangle to complement the existing scalene triangle and then subtract the area of the smaller right triangle from the bigger one (see picture).
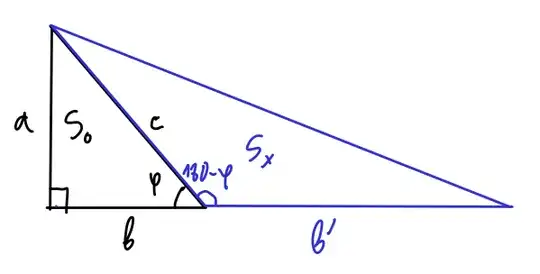
$$a=c\sin\phi$$ $$S_x=\frac{c \cdot \sin\phi \cdot (b+b')}{2}-\frac{c \cdot \sin\phi \cdot b}{2} = \frac{c \cdot \sin\phi \cdot b'}{2}$$ On the other hand, $$S_x=\frac{c \cdot \sin(\pi-\phi) \cdot b'}{2}$$ Thus, $$ \sin(\pi-\phi) = \sin \phi$$
I'll be grateful for any ideas/advice.