Medians of a triangle and the intersecting ratio

Question

Prove that any two medians of a triangle intersect in the ratio 2 : 1. I actually tried with median property but I don't know which theorem I should employ

Answer 1

Consider the triangle ABC below.

Let H$1$ and H$2$ halve the sides AC and BC, respectively. AH$1$ and BH$2$ are two medians which intersect ay S. The claim is that AS=2$\times$SH$2$ and BS=2$\times$SH$1$.

The line H$1$H$2$ is parallel to the line AB. ASB and H$1$SH$2$ are similar triangles because their angles are equal. Since AB=2$\times$H$1$H$2$, similarity implies that AS=2$\times$SH$2$ and that BS=2$\times$SH$1$ as claimed.

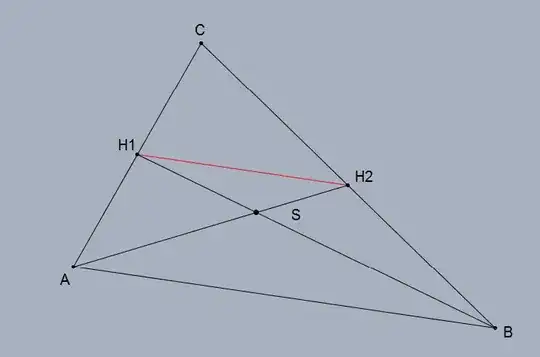
The argumentation above can be repeated with any pairs of midpoints of the sides.