8

I'm practicing with Winding Numbers, and encountered an interesting example. You might be familiar with this liantong symbol, the logo of China Unicom:

China Unicom

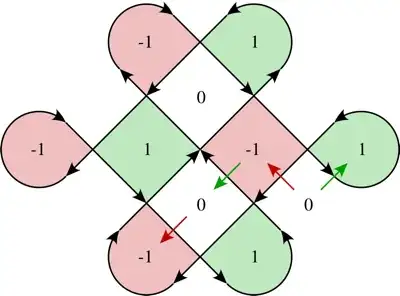
Suppose we make this into a fully closed and connected curve, and try to determine the Winding Numbers of the various points in the symbol. For instance:

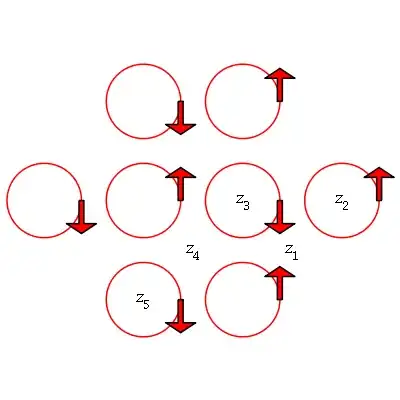
Find the winding numbers of the closed curve shown below at $z_1,z_2,z_3,z_4,z_5$

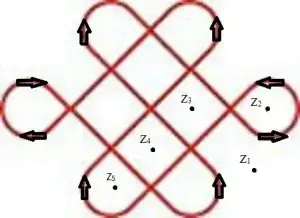
Winding Numbers of Liantong

It seems to me that for each $z$, the winding number $W(z)$ is:

  1. $W(z_1)=0$ (since it is outside the curve)
  2. $W(z_2)=1$ (since it falls to the left of the curve in one loop)
  3. $W(z_3)=-2$ (since it falls to the right of the curve in two loops)
  4. $W(z_4)=0$ (since it falls to the right and to the left of the curve twice each, cancelling out)
  5. $W(z_5)=-1$ (since it falls to the right of the curve in one loop)

Would you agree with these winding numbers (and given reasoning)? Thank you for your help!

EthanAlvaree
  • 3,518
  • 3
  • 31
  • 65
  • 1
    Crossing the curve (at a point where the curve doesn't intersect itself) changes the winding number by $\pm 1$. So the winding numbers of $z_1$ and $z_3$ must differ by $1$, not $4$. – Robert Israel Mar 18 '15 at 06:54
  • Okay, I agree with you that $W(z_3) \ne -4$. But when I trace the curve around $z_3$ I keep getting $W(z_3)=-2$ now. This one is tricky. – EthanAlvaree Mar 18 '15 at 07:12
  • $W(z_3)$ is definitely $-1$. But if you want to discuss it, you're going to have to label your intersection points. – TonyK Mar 18 '15 at 10:23

2 Answers2

10

If a curve crosses your path from left to right, the winding number increases.

If a curve crosses your path from right to left, the winding number decreases.

enter image description here

Going from $z_1$ to $z_2$, the curve crosses our path from left to right. Therefore, $\mathrm{W}(z_2)=1$.

Going from $z_1$ to $z_3$, the curve crosses our path from right to left. Therefore, $\mathrm{W}(z_3)=-1$.

Going from $z_3$ to $z_4$, the curve crosses our path from left to right. Therefore, $\mathrm{W}(z_4)=0$.

Going from $z_4$ to $z_5$, the curve crosses our path from right to left. Therefore, $\mathrm{W}(z_5)=-1$.

enter image description here

robjohn
  • 353,833
  • Great explanation! I didn't know it was this easy. I thought I had to trace the curve and keep track of the direction of every boundary around a point to see how the Winding number changes... This is a much simpler approach. Thank you! – EthanAlvaree Mar 18 '15 at 10:44
  • In essence, this method does just that. By noting the direction of the curve at each intersection with a path, we are keeping track of the direction at each boundary along the path. – robjohn Mar 18 '15 at 15:40
4

Note that the curve can be deformed to a union of clockwise and counterclockwise circles, which makes it much easier to find the winding numbers.

enter image description here

Robert Israel
  • 470,583