In Dugundji's book, chapter $V$, problems on section $1$, the $8$th problem says:
$Y$ is connected if and only if every open covering $\{U_{\alpha}\,|\,\alpha\in A\}$ of $Y$ has the following property: For each pair of sets $U_{\alpha_1},U_{\alpha_n}$, there are finitely many $U_{\alpha_2},\dots,U_{\alpha_{n-1}}$ such that $U_{\alpha_i}\cap U_{\alpha_{i+1}}\not=\emptyset$, $i=1,\dots,n-1$.
What I've paraphrased from this, is that if your space is connected then you can make a bridge from open set to open set using a finite number of open sets, something like this:
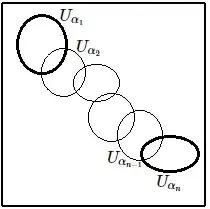
Proving the necessity wasn't that dificult, but proving the sufficiency is not very easy, mostly because I can't get to find a way to prove that you can find just $n$ open sets. If $Y$ is connected it's not necessarely compact, so I can't use that, and I can't figure a way to find a contradiction if we assume there is a covering which doesn't have the property, a lot of things can happen in that case, one of them is that there could be a infinite number of $U_{\alpha}$'s. Wouldn't we need more hypothesis?