15

I'm trying to solve exercise 5.6 in Steve Awodey's "Category Theory":

Show that a category with pull-backs and products has equalizers as follows: given arrows $f, g: A \to B$, take the pullback indicated below, where $\Delta = \langle 1_B, 1_B \rangle$:

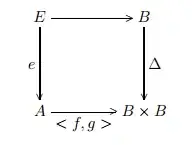
Diagram

Show that $e: E \to A$ is the equalizer of $f$ and $g$.

So I need to prove that $f \circ e = g \circ e$, and that given any $z: Z \to A$ with $f \circ z = g \circ z$ we can define a unique arrow such that $e \circ u = z$. How do I use the pullback property to do this?

Asaf Karagila
  • 405,794
Anne
  • 153

2 Answers2

9

Hint

Let's call $h: E \rightarrow B$. Now considering $B \times B$ from the definition know the existence of two maps $\pi_1, \pi_2 : B \times B \rightarrow B$ such that:

$\pi_1 \circ \langle f,g \rangle = f$

$\pi_2 \circ \langle f,g \rangle = g$

Knowing this we can see:

$f \circ e = \pi_1 \circ \langle f,g \rangle \circ e = \pi_1 \circ \Delta \circ h = h= \pi_2 \circ \Delta \circ h = \pi_2 \circ \langle f,g \rangle \circ e = g \circ e$

Smiley1000
  • 4,219
Abellan
  • 3,835
  • 15
  • 35
2

To complete the Abellan's answer: If $z:Z\rightarrow A$ is a morphism such that $f\circ z=g\circ z$.

Propose, $z:Z\rightarrow A$ and $f\circ h: Z\rightarrow B$.

Remember that product's projections are mono-source. So If two morphims are equal when composited with the projections, they are equal.

$\pi_{1}\circ \langle f,g \rangle \circ z=f\circ z$

$\pi_{1}\circ\Delta_{B}\circ f\circ z= 1_{B}\circ f\circ z=f\circ z$

$\pi_{2}\circ \langle f,g \rangle \circ z=g\circ z$

$\pi_{2}\circ \Delta_{B}\circ f\circ z= f\circ z$

But, by hypotesis, $g\circ z= f\circ z$.

From the pullback's propierties, we have that exist unique arrow $u$ such that $e\circ u=z$.

Smiley1000
  • 4,219
RNopalzin
  • 107