The functions $x$ and $x^2 - {1\over2}$ are orthogonal with respect to their inner product on the interval [0, 1]. However, when you graph the two functions, they do not look orthogonal at all. So what does it truly mean for two functions to be orthogonal?
Consider these two functions defined on a grid of $x\in\{1,2,3\}$:
$$f_1(x)=\sin\left(\frac{\pi x}2\right),$$ $$f_2(x)=\cos\left(\frac{\pi x}2\right).$$
Their plot looks like
If you look at their graph, they don't look orthogonal at all, as the functions plotted in the OP. Yet, being interpreted as vectors $(1,0,-1)^T$ and $(0,-1,0)^T$, they are indeed orthogonal with respect to the usual dot product. And this is exactly what is meant by "orthogonal functions" — orthogonality with respect to some inner product, not orthogonality of the curves $y=f_i(x)$.
Function spaces that have an inner product and are complete under the induced norm, i.e. Hilbert spaces, have their own sort of infinite-dimensional geometry. One should consider "functions" that belong to such a function space as "points" lying in an infinite-dimensional geometric space. In such spaces, the notion of "orthogonal functions" is interpreted geometrically, analogous to how in finite-dimensional Euclidean space we have a geometric notion of "orthogonal vectors."
Orthogonal vectors in a Hilbert space are, just like in Euclidean space, sort of the "most" linearly independent you can get. In Euclidean space, if $a$ and $b$ are vectors, then one can take the projection of $a$ onto $b$, say $p(a,b)$, and then one can write $a = p(a,b) + o(a,b)$, where $o(a,b)$ is the part of $a$ orthogonal to $b$. When $a$ and $b$ are orthogonal, $p(a,b)$ vanishes and you just have the orthogonal part $o(a,b)$, so in this sense no part of $a$ belongs to the subspace generated by $b$.
The same exact thing happens in infinite-dimensional Hilbert spaces (note my argument above used nothing about finite dimensions). We can't really draw infinite-dimensional space, so this geometric notion of orthogonality is interpreted abstractly.
Since the inner product is $\left<f,g\right>=\int_{0}^{1}f(x)g(x)\mathrm{d}x$, then orthogonality means that the integral over the interval $[0,1]$ is zero.
The way in which the functions are orthogonal has only a very abstract resemblance to the way in which vectors in $\Bbb R^2$ are orthogonal. It does not mean that the graphs are geometrically orthogonal in any way; functions are not the same as their graphs. You should think of "orthogonal" as a metaphor: the functions are orthogonal because their inner product is zero. This is analogous to, but not the same as, the way two vectors in $\Bbb R^2$ point in geometrically perpendicular directions if their inner product (a different inner product) is zero.
Mathematics works by identifying common patterns and understanding them in a way that is at once more general and more abstract. By generalizing and abstracting the notion of the orthogonality of two vectors, we can apply the techniques of linear algebra to function spaces.
Functions can be added together, scaled by constants, and taken in linear combination--just like the traditional Euclidean vectors.
$$\vec{u} = a_1\vec{v}_1 + a_2\vec{v}_2 + \cdots a_n\vec{v}_n$$
$$g(x) = a_1f_1(x) + a_2f_2(x) + \cdots + a_nf_n(x) $$
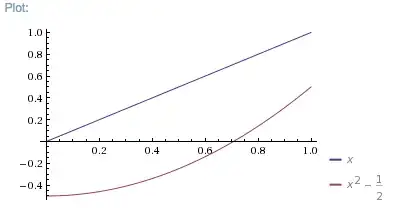
Just as $\left( \begin{array}{c} 5\\ 2\\ \end{array} \right) = 5\left( \begin{array}{c} 1\\ 0\\ \end{array} \right) + 2\left( \begin{array}{c} 0\\ 1\\ \end{array} \right) $, I can say $5x + 2x^2 - 1 = 5(x) + 2(x^2 - \frac{1}{2})$
"Orthogonality" is a measure of how much two vectors have in common. In an orthogonal basis, the vectors have nothing in common. If this is the case, I can get a given vector's components in this basis easily because the inner product with one basis vector makes all other basis vectors in the linear combination go to zero.
If I know $\left( \begin{array}{c} 1\\ 0\\ 0.5\\ \end{array} \right)$, $\left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right)$ and $\left( \begin{array}{c} 2\\ 0\\ -4\\ \end{array} \right)$ are orthogonal. I can quickly get the components of any vector in that basis:
$$\left( \begin{array}{c} 8\\ -2\\ 5\\\end{array} \right) = a\left( \begin{array}{c} 1\\ 0\\ 0.5\\ \end{array} \right) + b\left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right) + c\left( \begin{array}{c} 2\\ 0\\ -4\\ \end{array} \right)$$
$$\left( \begin{array}{c} 1\\ 0\\ 0.5\\ \end{array} \right) \cdot \left( \begin{array}{c} 8\\ -2\\ 5\\\end{array} \right) = \left( \begin{array}{c} 1\\ 0\\ 0.5\\ \end{array} \right) \cdot \big[ a\left( \begin{array}{c} 1\\ 0\\ 0.5\\ \end{array} \right) + b\left( \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right) + c\left( \begin{array}{c} 2\\ 0\\ -4\\ \end{array} \right) \big]$$
I know the $b$ and $c$ term disappear due to orthogonality, so I set them to zero and forget all about them.
$$8.25 = 1.25 a$$
I can also get function basis components easily this way. Take the fourier series on $[0,T]$ for example, which is just a (infinitely long) linear combination of vectors/functions:
$$ f(x) = a_0 + \sum_n^\infty a_ncos(\frac{2\pi n}{T}x) + \sum_n^\infty b_nsin(\frac{2\pi n}{T}x) $$
I know that all the $cos$ and $sin$ basis functions are orthogonal, so I can take the inner product with $cos(\frac{2\pi 5}{T}x)$ and easily get a formula for the $a_5$ coefficient because all the other terms vanish when I do an inner product.
$$\int cos(\frac{2\pi 5}{T}x) f(x) dx = a_5 \int cos^2(\frac{2\pi 5}{T}x) dx$$
Of course I could do this in general with $cos(\frac{2\pi q}{T}x)$ to get any of the $a_q$ components.
