3

Let f be a non-negative continuous function on $[0,\infty)$.

If it's given that: $$\lim_{x \to \infty}\int_{x}^{x + 1}f(t)dt = 0$$

Does it follow that: $$(*) \ \lim_{x \to \infty}f(x) = 0 ?$$

Why or why not?

I (thought) I had solved this problem, but it was pointed out that my argument was flawed. To prove $(*)$, I reasoned as follows:

$f$ is continuous, so by MVT, there exists $C_x$ in $[x,x+1]$, such that:

$$\int_{x}^{x + 1}f(t)dt = f(C_x)\int_{x}^{x + 1}dt = f(C_x)$$

So it follows that:

$$\lim_{x \to \infty}f(x) = \lim_{x \to \infty}f(C_x) = \lim_{x \to \infty}\int_{x}^{x + 1}f(t)dt = 0 $$

What is missing in my work? Or where had I gone wrong?

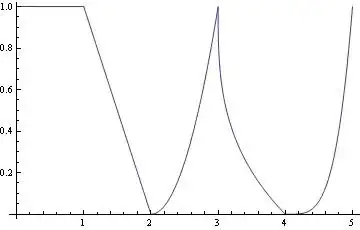
In case I'm mistaken and $(*)$ doesn't hold, in general, please present a counter-example and explain to me where had I gone wrong.

Thanks a lot.

Community
  • 1
  • 3
    It is false. Now knowing that, can you think of a counter example? If not I'll post one as an answer. – Simon S Feb 14 '15 at 19:31
  • 1
    Regarding the result cf to @SimonS. Regarding your reasoning: from $f(C_x)\rightarrow 0$ you cannot conclude anything about the behavior of $f$, unless you impose additional assumptions (like, e.g., monotonicity). – Thomas Feb 14 '15 at 19:36
  • @SimonS, if possible, please do. And it would be kind of you to explain why my argument is erroneous. –  Feb 14 '15 at 19:49
  • I think, once you have a counterexample, you will be able to find out why the argument is erroneous. – user 59363 Feb 14 '15 at 20:04
  • @user59363 has basically given it below. Form instead isosceles triangles over bases of length $1/n$. That gives continuity. Now see how that makes your argument fail. – Simon S Feb 14 '15 at 20:05
  • Don't ask questions and delete them moments later. It wastes everyone's time. (I'm referring to a different question here.) – copper.hat Feb 19 '15 at 18:24

3 Answers3

3

Another hint: take first a function which takes the value $0$ on every interval of the form $(n+\frac{1}{n}, n+1]$ and $1$ on every interval of the form $(n, n+\frac{1}{n}]$. This function satisfies the requirement for the integral, however it is not continuous. Can you perhaps change the values in the intervals $(n,n+\frac{1}{n}]$ so that the resulting function is contiuous and the requirement on the integral is still satisfied, but e.g. $f(n+\frac{1}{2n})=1$ for all $n$, so that $\lim_{x\to \infty}f(x)$ does not exist?

You can modify this to construct a function $f$ that serves your purpose and satisfies even $\limsup_{x\to \infty} f(x)=\infty$.

user 59363
  • 1,464
1

Take $f(x)=sin(2\pi x)$. This function satisfies $f(x+1/2)=-f(x)$, so $\int_x^{x+1}f(t)dt=\int_x^{x+1/2}f(t)dt+\int_{x+1/2}^{x+1}f(t)dt=\int_x^{x+1/2}f(t)dt+\int_x^{x+1/2}f(t+1/2)dt=\int_x^{x+1/2}f(t)dt-\int_x^{x+1/2}f(t)dt=0$, so clearly $\lim_{x\rightarrow\infty}\int_x^{x+1}f(t)dt=0$, but $\lim_{x\rightarrow\infty}f(x)$ doesn't exist.

Wojowu
  • 27,526
0

Consider the function $f(x)$ defined as follows: $1$ on $[0,1]$, $1-(x-1)$ on $[1,2]$, $(x-2)^{2}$ on $[2,3]$, and so on. In general, let $(x-2n)^{2n}$ on $[2n,2n+1]$ and $1-\sqrt[2n+1]{x-(2n+1)}$ on $[2n+1,2n+2]$ for $n=0,1,\cdots$. Draw the picture and try to figure out the area under the curve on any interval $[x,x+1]$ for $x\geq0$.

enter image description here

We can see that $\lim_{x\to\infty}\int_{x}^{x+1}f(u)\mathrm{d}u=0$ however $f(2n+1)=1$ for all $n=0,1,\cdots$, which implies that $\lim_{x\to\infty}f(x)$ cannot be $0$.

bkarpuz
  • 845