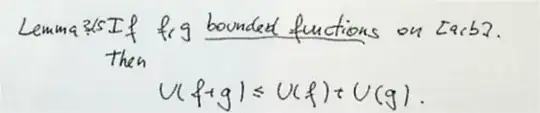$U$ here represents the upper Riemann Integral.
I understand the vast majority of this proof, however the part underlined in orange states $\forall \varepsilon>0 $ should it not be $\forall \varepsilon\geq0 $ so that we have
$U(f)\leq S(f,\Delta_\varepsilon ^1) \leq U(f)+\frac{\varepsilon}{2}$?
For the green part , if the statement works $\forall\varepsilon>0$ surely it could work in the case $U(f+g)=50$, $U(f)+U(g)=49$, $\varepsilon=2$
It should be $\forall\varepsilon>0:U(f)\leq S(f,\Delta_\varepsilon ^1) <U(f)+\frac{\varepsilon}{2}$, if you want to employ the definition (of infimum) precisely, though it's not a big issue here that equality is included.
P.S.: $\varepsilon$ is used almost always for a positive number.
First note if $\epsilon$ = 0, then $\Delta_{\epsilon} \equiv$ 0, and we have something uninteresting: $$ \ S(f+g,\Delta) = \displaystyle\sum_{k}^{n-1} M_{k}(f+g)(x_{k+1} - x_{k}) = \displaystyle\sum_{k}^{n-1} M_{k}(f+g)(0) \equiv 0 $$ Otherwise if we don't permit equality, we can recover the definition of the upper integral as $\Delta_{\epsilon} \rightarrow 0$. That is $$ \ (U) \int^{a}_{b} f \ dx = \inf \{U(f,\Delta_{\epsilon}) | \text{where} \Delta_{\epsilon} \text{is any partition of [a,b]}\} $$ But $\Delta_{\epsilon} \neq 0$, so as Uzman writes, $U(f)\leq S(f,\Delta_\varepsilon ^1) < U(f)+\frac{\varepsilon}{2}$
Moreover, $\epsilon > 0$ by convention. If not, we would have many trivial results.
In regard to the green box, what you write is not exactly correct, the inequality must hold for all $\epsilon > 0$, that's the beauty. Any value you want, there is another value, smaller yet, that the inequality holds for.
