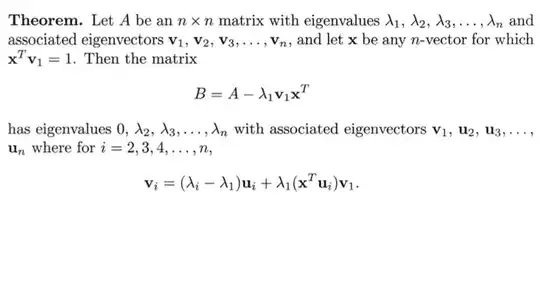Given a real-valued matrix $A$, one can obtain its largest eigenvalue $\lambda_1$ plus the corresponding eigenvector $v_1$ by choosing a random vector $r$ and repeatedly multiplying it by $A$ (and rescaling) until convergence.
Once we have the first eigenpair, is there a similar way to estimate the second eigenpair?
Here is a theorem that you can use:
where $$\vec{x}=\frac{1}{\lambda_1 v_{1,k}}\begin{pmatrix} a_{k1}\\ a_{k2}\\ ...\\ a_{kn} \end{pmatrix}$$
$v_{1,k}$ is the $k$th component of $\vec{v}_1$, $a_{ki}$ is the $ki$th element of $A$. The row $k$ is smallest index such that $v_{1,k}$ is the infinity norm of $\vec{v}$, i.e., the largest component.
Then you can find the largest eigenvalue of $B$, which is the second largest of $A$.
$A=\sum_{i=1}^n \lambda_i v_iv_i^\top$ where $(\lambda_i,v_i)$ are the eigenvalue/vector pairs of $A$.
So, if you know that $|\lambda_1| \ge |\lambda_2| \ge \dots \ge |\lambda_n|$, then you can obtain $\lambda_2$ by computing the largest eigenvalue/vector pair in absolute value of $$B=A-\lambda_1 v_1v_1^\top$$
The method is called deflation. The link provided by KittyL seems failed. Just in case someone need a ref, here is anthor source for the method:
https://services.math.duke.edu/~jtwong/math361-2019/lectures/Lec10eigenvalues.pdf
