2

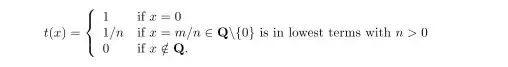
Given the Thomae Function: $$t(x)= \begin{cases} 1 & \text{if }x=0, \\ 1/n & \text{if }x=m/n \in \mathbf Q\setminus\{0\}\text{ is in lowest terms with }n>0,\\\ 0 & \text{if }x\notin\mathbf Q. \end{cases} $$ enter image description here

I am trying to do the following exercise:

Exercises 4.2.4. Review the definition of Thomae's function $t(x)$ from Section 4.1.
(a) Construct three difference sequences $(x_n)$, $(y_n)$ and $(z_n)$, each of which converges to $1$ without using the number $1$ as a term in the sequence.
(b) Now, compute $\lim t(x_n)$, $\lim t(y_n)$ and $\lim t(z_n)$.
(c) Make an educated conjecture for $\lim_{x\to1}t(x)$, and use Definition 4.2.1B to verify the claim. (Given $\epsilon>0$ consider the set of points $\{x\in\mathbf R \colon t(x)\ge\epsilon\}$. Argue that all the points in this set are isolated.)

enter image description here

I have no difficulties with part a) and b), and the conjecture for part c) is that $$\lim_{x \to 1} t(x) = 0$$ I am pretty sure with this conclusion. However, I do not know how to use the definition 4.2.1B, which is the topological version of the functional limits and it is stated as following: $\lim_{x \to 1} t(x) = 0$ if $\exists \delta \gt 0$ such that whenever $x \in V_{\delta}(1)$,$\forall \epsilon \gt 0$ $t(x) \in V_{\epsilon}(0)$ . That is what we want to prove.

Please help me prove that $\lim_{x \to 1} t(x) = 0$ using topological definition of functional limits. I thank you very much for your help.

EXTRA QUESTION: I found this kind of solution: enter image description here

However, there are 3 things I do not understand:

  1. If $\epsilon = 2$, then $n \le \frac{1}{\epsilon}=\frac{1}{2}$. Then there is no $n$ since $n$ must be a natural number. How do we explain this situation?

2.I do not understand why we take $\delta=\min\{y: y \in T \cap \left[0,2\right]\}$

  1. Why if $x \in V_{\delta}(1)$, then $x \notin T$ ? This is the most peculiar question that baffles me for hours.

I thank you very much for your explanation.

Martin Sleziak
  • 56,060
SON TO
  • 653
  • 5
  • 13

1 Answers1

2

Notice the following:

$$1-\frac{1}2<1-\frac{1}3<1-\frac{1}4<\ldots<1-\frac{1}n<\ldots<1<\ldots<1+\frac{1}n<\ldots < 1+\frac{1}3<1+\frac{1}2.$$ That is to say, every rational other than $1$ in $(1-\frac{1}n,1+\frac{1}n)$ has denominator of at least $n+1$, thus, for $x$ in that interval, $t(x)<\frac{1}n$. Now, if you choose some $n$ such that $\frac{1}n<\varepsilon$, you can easily complete the proof.

Milo Brandt
  • 61,938
  • Thanks Meelo! I have proved the theorem now. However, it uses the concepts of functional limits in a functional way, not topological way where we use $V_{$/epsilon$}(x)$ as $\epsilon$ neighborhood of x. – SON TO Jan 20 '15 at 07:02